Найти наибольшее и наименьшее значение функции,фото прикреплено,я бестолочь,помогите пожалуйста,заранее спасибо
Приложения:
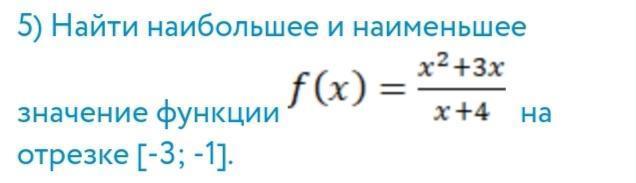
Ответы
Ответ дал:
1
Производная функции равна
приравняем к нулю :
одз: х не равен -4
числитель приравняем к нулю
дискриминант равен 16
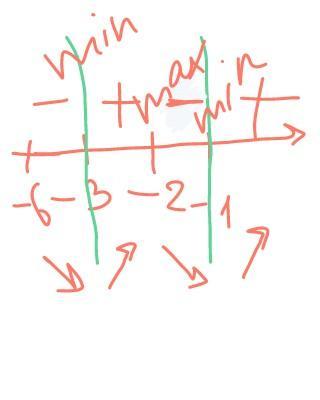
корни равны -6 и -2
подставим - 3 , у= -3
подставим -2 ,у=0
подставим -1 ,у=5/9
наименьшее значение -3
наибольшее значение 5/9
Приложения:
dariaruban11:
спасибочки,вы очень-очень мне помогли,хорошего вечера
Ответ дал:
1
Объяснение:
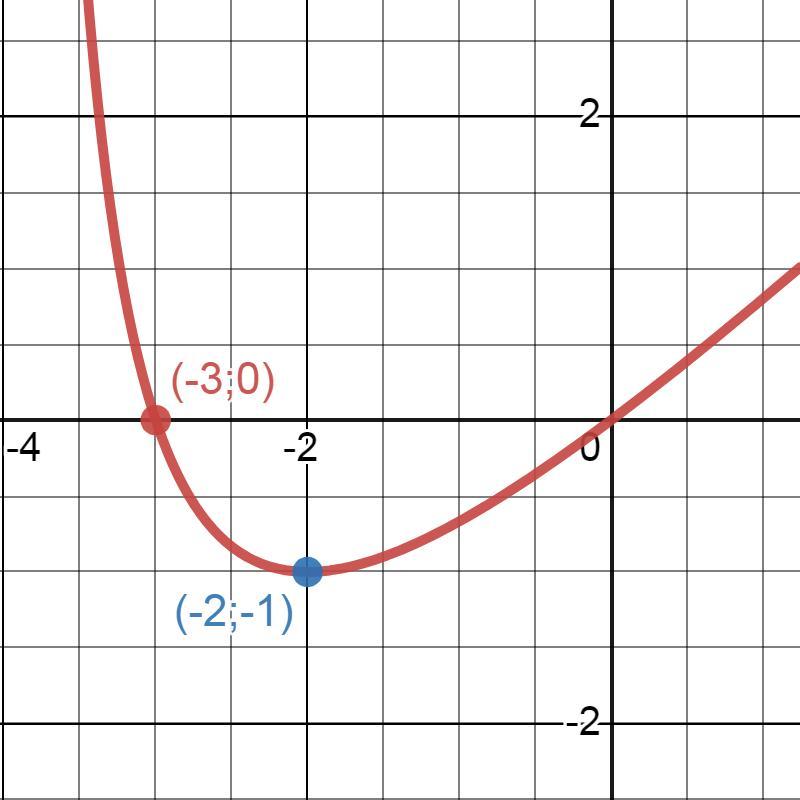
Ответ: f(-3)=0=наиб. f(-2)=-1=наим.
Приложения:
спасибо огромнейшее!!!!
Удачи.
Вас заинтересует
2 года назад
2 года назад
2 года назад
2 года назад
8 лет назад
9 лет назад