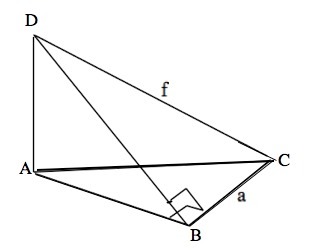
В треугольнике ABC угол В прямой и катет BС = а. Из вершины А проведён к плоскости треугольника перпендикуляр AD так, что расстояние между точками D и С равно f. Определить расстояние от точки D до катета ВС.
Пожалуйста полное решение+рисунок)
Ответы
Ответ дал:
0
Расстояние от точки до прямой равно длине отрезка. проведенного из точки перпендикулярно к этой прямой.
По условию ∆ АВС - прямоугольный. АВ⊥ВС.
АВ – проекция наклонной DB. По т. о 3-х перпендикулярах:
Прямая , лежащая в плоскости, перпендикулярна наклонной тогда и только тогда, когда она перпендикулярна проекции этой наклонной на данную плоскость.
ВС⊥АВ⇒ ВС⊥DB.⇒ ∠DBC=90°
Треугольник DBC прямоугольный, DC- его гипотенуза.
По т.Пифагора DB=√(DC²-BC²)=√(f²-a²)
Приложения:
Вас заинтересует
2 года назад
2 года назад
8 лет назад
10 лет назад
11 лет назад