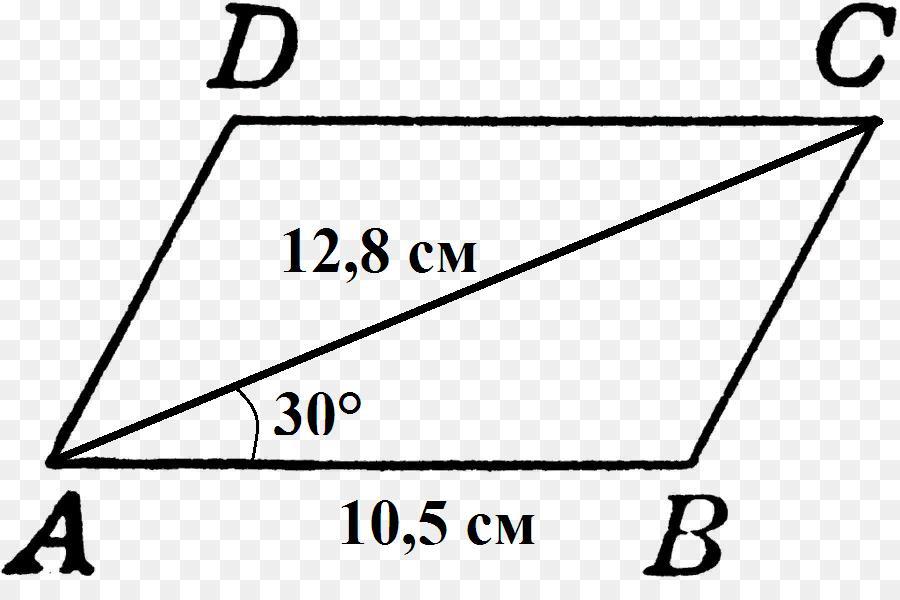
В параллелограмме основание и диагональ образуют угол в 30 ° . Найди площадь параллелограмма , если известно , что основание параллелограмма равно 10,5 см , а диагональ на 2,3 см больше стороны .
Ответы
Ответ дал:
1
Диагональ параллелограмма делит его на два равновеликих (одинаковых по площадь) треугольника. Площадь треугольника вычисляется по формуле: S=a*b*sinα/2, тогда площадь параллелограмма - S=a*b*sinα, где а - сторона параллелограмма, b - диагональ, α - угол между ними;
а=10,5 см;
b=10,5+2,3=12,8 см;
α=30°;
S=10,5*12,8*sin30°=67,2 см².
Приложения:
qwertyqwerty23qwerty:
спасибо большое!
https://znanija.com/task/49583895
осталось только колонку найти...
Как 3 разделилось на 1;1;2? https://znanija.com/task/49585168
Вас заинтересует
2 года назад
2 года назад
2 года назад
8 лет назад
9 лет назад
9 лет назад