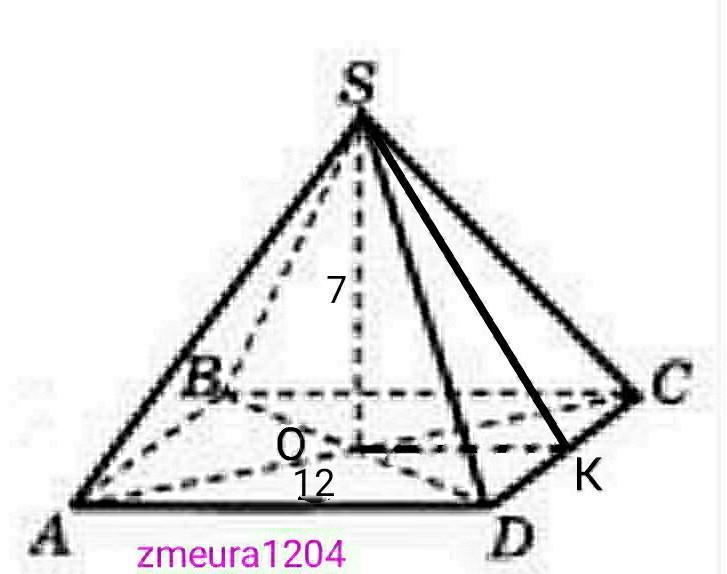
Найдите площадь боковой поверхности правильной четырехугольной пирамиды сторона основание которой равно 12 и высота равна 7
с рисунком
Ответы
Ответ дал:
1
Ответ:
24√85 ед²
Решение:
ОК=АD/2=12/2=6 ед.
∆SOK- прямоугольный треугольник.
По теореме Пифагора
SK=√(SO²+OK²)=√(6²+7²)=
=√(36+49)=√85 ед.
Sбок=½*Росн*SK;
Pосн=4*АВ=4*12=48 ед
Sбок=½*48*√85=24√85 ед²
Приложения:
tanushkash05:
спасибо большое
Пожалуйста.
Вас заинтересует
2 года назад
2 года назад
9 лет назад