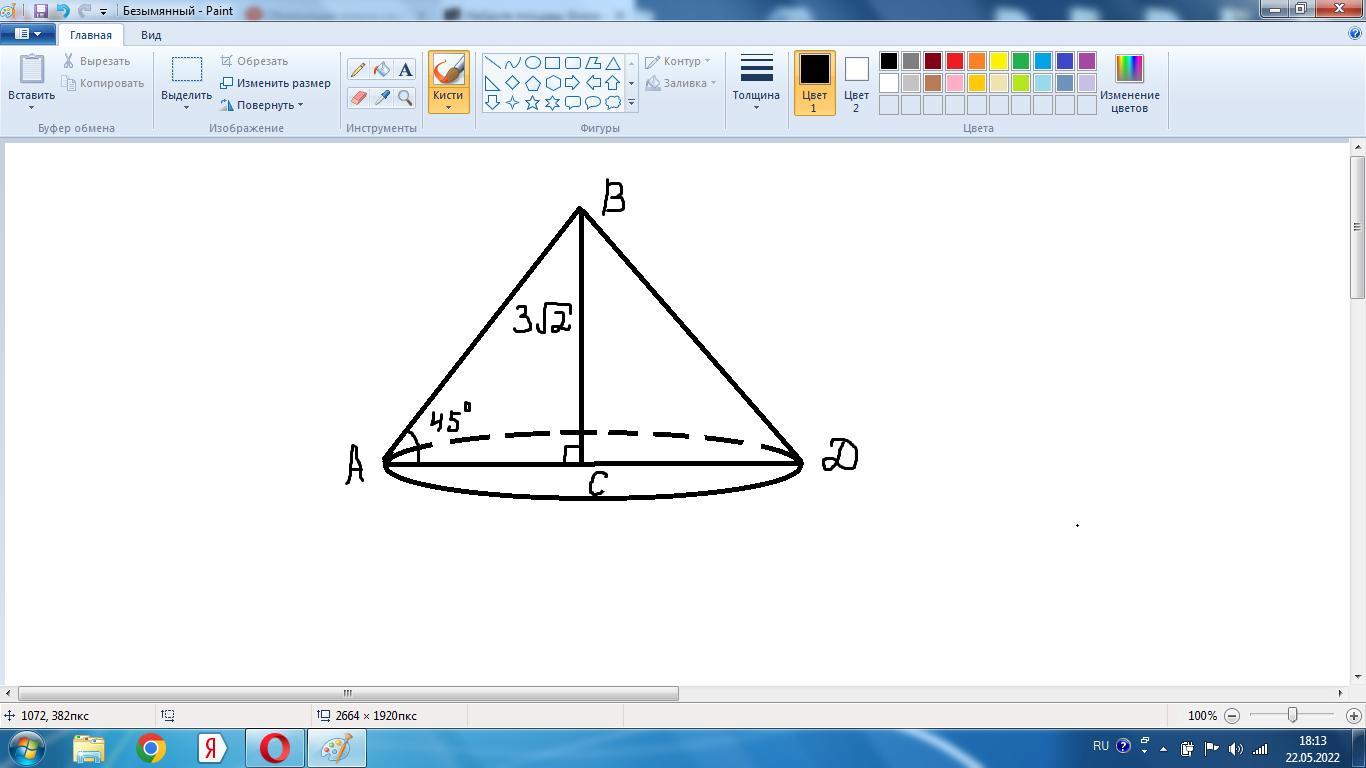
Образующая конуса составляет с плоскостью основания угол 45, высота конуса равна 3√2 см. Найдите площадь боковой поверхности конуса.
lizapivnenko5:
угол 45 град.э
Ответы
Ответ дал:
3
Ответ:
Δ ВСA - прямоугольный.
Так как ∠ВАС=45°, то Δ равнобедренный.
Радиус основания СА = 3√2 см
________________________________________________
По теореме Пифагора найдем образующую конуса ВA:
ВA² = (3√2)² + (3√2)²
ВA² = 18 + 18
ВA² = 36
ВA = 6 см
Площадь боковой поверхности конуса:
S(бок.) = п * r * l = 6 * 3√2 *п = 18√2п см²
Приложения:
Добрый вечер не могли бы мне помочь с геометрией пожалуйста
Вас заинтересует
2 года назад
2 года назад
2 года назад
8 лет назад
8 лет назад