Ответы
Ответ дал:
1
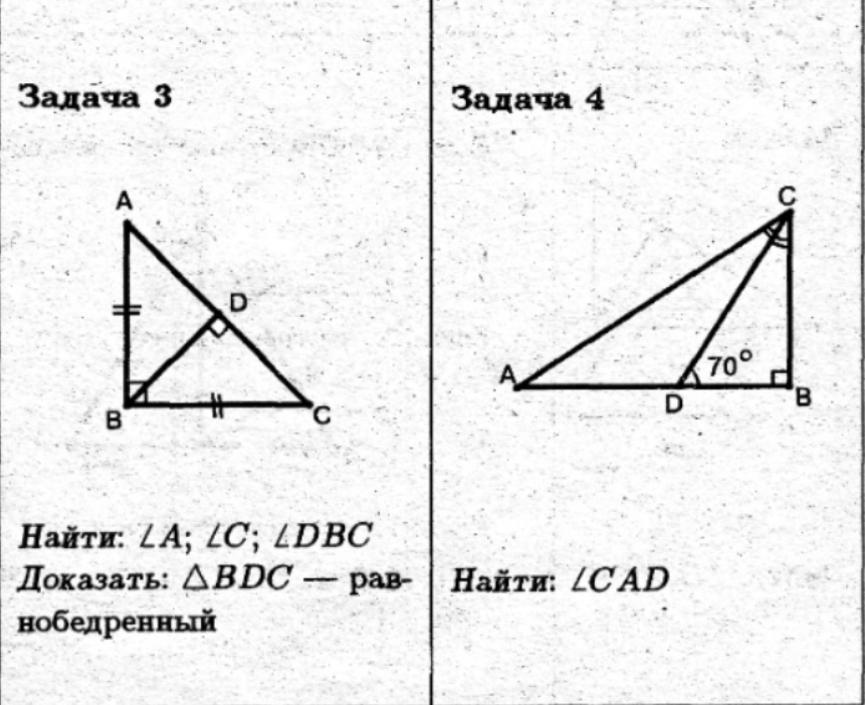
Задача 3
Так как AB=BC, то Δ ABC - равнобедренный, а ∠B = 90°, то Δ ABC - прямоугольный
если Δ ABC - равнобедренный, то углы при основании равны: ∠A=∠C
Пусть x =∠A=∠C,
тогда ∠B+∠A+∠C=180
x+x+90=180
2x=180-90
2x=90
x=90/2=45
∠A=∠C=45°
так как ∠BDC = 90°, значит, Δ BDC
∠DBC = 90-∠C=90-45=45°
∠DBC=∠C=45°, то BD=DC, а Δ DBC является равнобедренным
Ответ. ∠A=∠C=∠DBC=45°
Задача 4
так как ∠B = 90°, то ΔBDC - прямоугольный, а, значит, что острых сумма углов равна 90°
∠ACD = ∠DCB по условию
⇒ ∠DCB=90-∠CDB=90-70=20°
∠ACD = ∠DCB =20°
∠CDB и ∠CDA - смежные
⇒ ∠CDB+∠CDA=180°
⇒∠CDA=180-∠CDB=180-70=110°
сумма всех углов в треугольнике равна 180 °
Следовательно, ∠CAD=180-(∠ACD+∠CDA)=180-(110+20)=180-130=50°
Ответ. ∠CAD = 50°
Лучший ответ пж
socol1241:
СПАСИБО ЧЕЛ
НЕ ЗА ЧТО ЧЕЛ
Вас заинтересует
2 года назад
2 года назад
2 года назад
8 лет назад
8 лет назад
9 лет назад