Ответы
Ответ дал:
1
Ответ:
Объяснение:
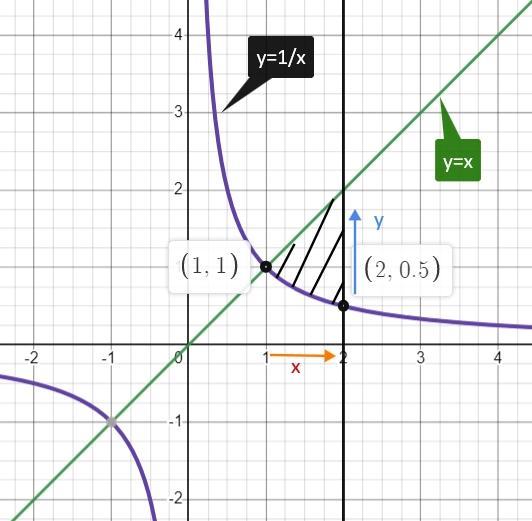
Прежде всего сделаем чертеж и определим область интегрирования.
Потом я стрелками отметила, как изменяется х (красная стрелка) и как изменяется у (синяя стрелка).
х изменяется от 1 до 2 - вполне себе числа,
у изменяется от 1/х до х - это уже переменные.
Это записывается в виде неравенств
1 ≤ х ≤ 2
1/х ≤ у ≤ х
Таким образом, мы получили порядок обхода области интегрирования или "порядок интегрирования".
Вот, собственно и всё.
Осталось только записать повторный интеграл
Приложения:
Вас заинтересует
2 года назад
2 года назад
2 года назад
9 лет назад
