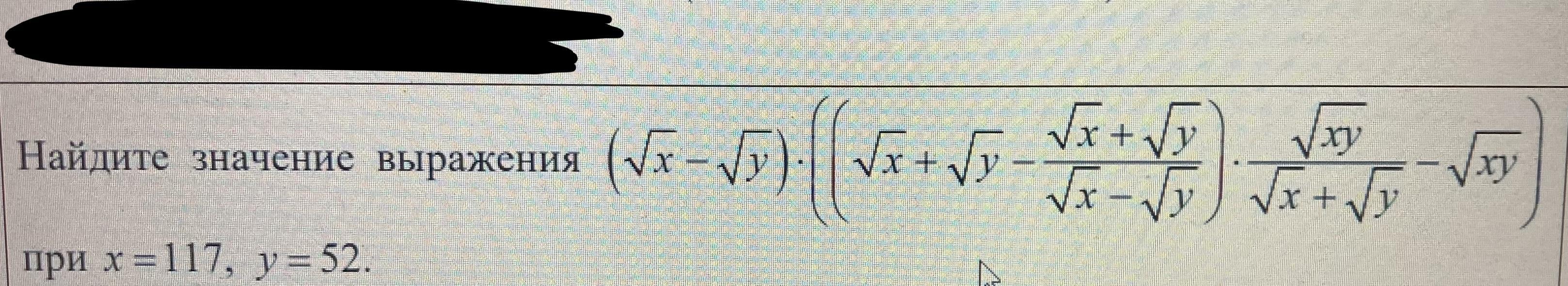Ответы
Ответ дал:
2
Ответ:
–78
Объяснение:
Требуется найти значение выражения
при x=117, y=52.
Решение. Сначала упростим выражение:
Теперь подставляем заданные значения:
#SPJ1
Вас заинтересует
1 год назад
2 года назад
7 лет назад
7 лет назад
9 лет назад