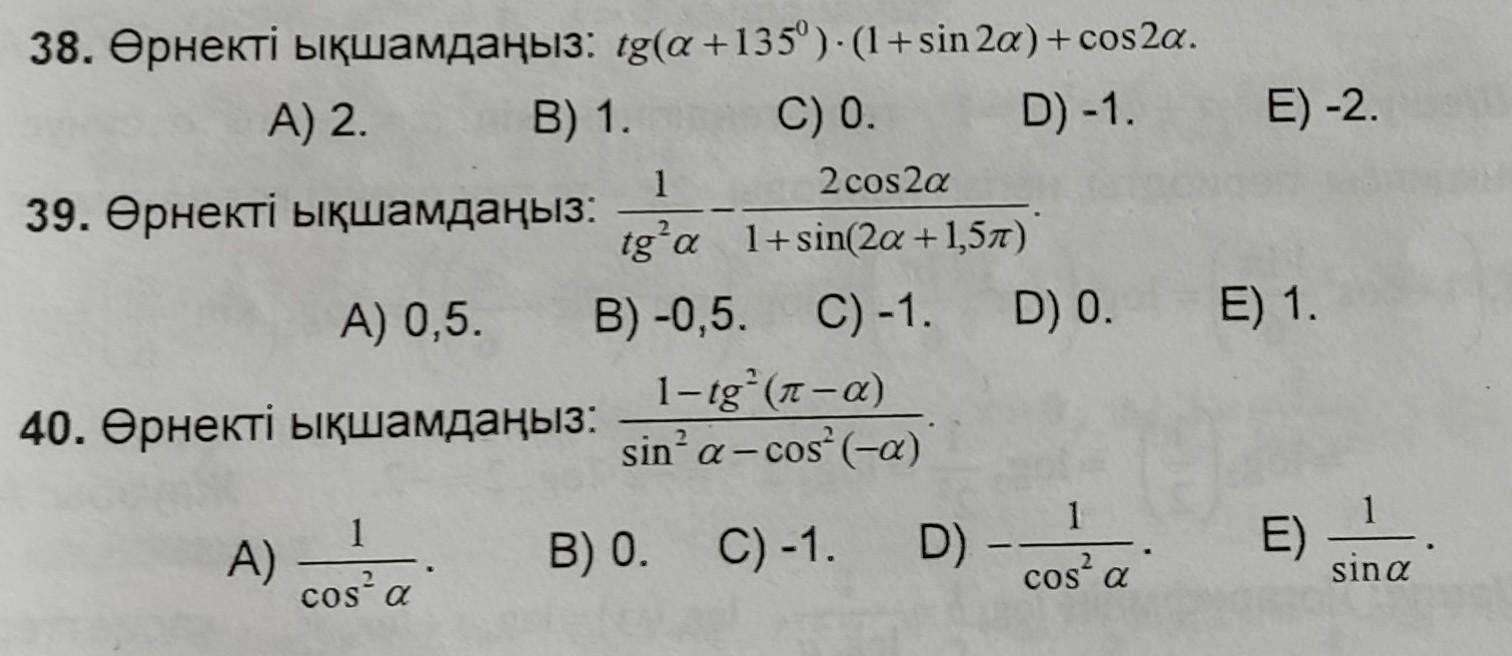Ответы
Ответ дал:
0
Ответ:
1) Применяем формулы приведения , формулы
синуса и косинуса двойных углов .
Ответ: С) .
2) Применяем формулу приведения и формулу
понижения степени .
Ответ: Е) .
3) Применяем формулу приведения и формулу
косинуса двойного угла .
Ответ: D) .
meizum3s162g74:
у меня севодне очень важная кр по алгебре 7 клас поможеш
??
нет
ахахахахахахах
помогите пожалуйста решить задачу интеграл
Помогите пожалуйста https://znanija.com/task/49609356
Вас заинтересует
2 года назад
2 года назад
2 года назад
2 года назад
8 лет назад
8 лет назад
9 лет назад