Дано дифференциальное уравнение второго порядка, которое
допускает понижение порядка. Найти частное решение, которое
удовлетворяет заданным начальным условиям.
Приложения:
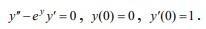
Ответы
Ответ дал:
0
Ответ:
Объяснение:
Есть стандартный способ решения таких задач (в уравнении явно нет x, поэтому теория рекомендует замену
Но конкретно эту задачу можно сделать проще: заметим, что
поэтому уравнение можно записать в виде
подставляя начальные условия, получаем
1=1+С⇒ C=0;
подставляя начальные условия, получаем -1=0+С⇒ С=-1;
arina271997:
спасибо огромное. Помогите еще с этим https://znanija.com/task/49675034 Я в этой теме полный ноль
пожалуйста
Вас заинтересует
2 года назад
2 года назад
2 года назад
8 лет назад
9 лет назад