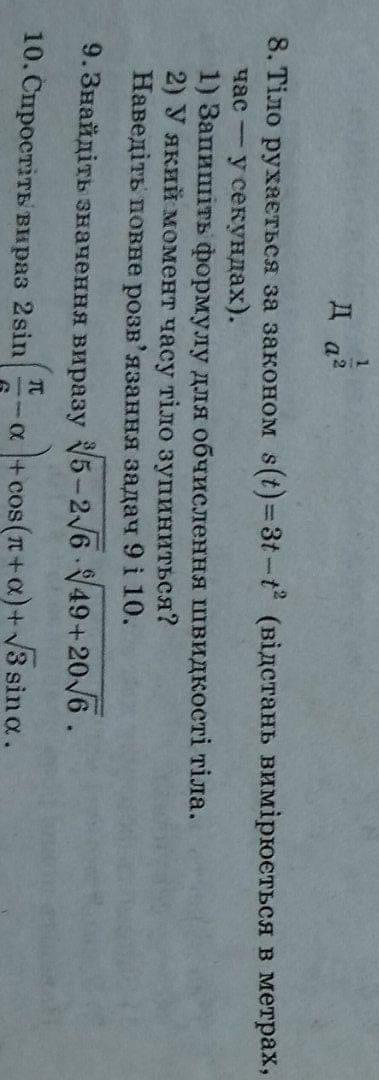Question

ПОМОГИТЕ СРОЧНО ДАЮ 30 БАЛОВ!!!!​

Answer 1

8) Тело движется по закону заданному функцией S(t)=3t-t^2. Найти формулу для вычисления скорости тела и определить, в какой момент времени тело остановится, если время t измеряется в секундах, расстояние S - в метрах.

9) Найти значение выражения $\large \boldsymbol {} \sqrt[3]{5-2\sqrt{6} } *\sqrt[6]{49+20\sqrt{6} }$

10) Упростить выражение 2sin (π/6 - α) + cos (π + α) + √3sin α.

Ответ:

8) Формула для вычисления скорости тела: 3-2t. Тело остановится в момент времени t=1,5с.

9) Значение выражения равно единице.

10) Значение выражения равно нулю.

Объяснение:

8) Если материальная точка движется неравномерно по закону заданному функцией y=S(t), то мгновенная скорость движения в момент времени а - значение производной функции S(t) в точке а.

$\LARGE \boldsymbol {} S'(t)=v(t)=(3t-t^2)'=(3t)'-(t^2)'=\\\\=3*1-2t^{2-1} =\boxed{3-2t}$

Определим в какой момент времени тело остановится (скорость будет равна нулю).

$\LARGE \boldsymbol {} 3-2t=0\\\\-2t=-3\\\\\boxed{t=1,5}$

$\Large \boldsymbol {} 9)\ \sqrt[3]{5-2\sqrt{6} } *\sqrt[6]{49+20\sqrt{6} }$

Для удобства распишем сначала второй корень отдельно, а потом вернёмся к выражению

$\LARGE \boldsymbol {} \sqrt[6]{49+20\sqrt{6} } = \sqrt[6]{25+20\sqrt{6} +24} =\\\\=\sqrt[6]{\underset{a^2}{\underbrace{5^2}}+\underset{2ab}{\underbrace{10*2\sqrt{6}}}+\underset{b^2}{\underbrace{(2\sqrt{6} )^2}} } =\sqrt[6]{(5+2\sqrt{6})^2 }$

Мы пришли к тому что $\large \boldsymbol {} \sqrt[6]{49+20\sqrt{6} }=\sqrt[6]{(5+2\sqrt{6})^2 }$. Подставляем в изначальное выражение.

$\Large \boldsymbol {} \sqrt[3]{5-2\sqrt{6} }*\sqrt[6]{(5+2\sqrt{6})^2 } = \sqrt[3]{5-2\sqrt{6} }* \sqrt[3]{5+2\sqrt{6} }=\\\\= \sqrt[3]{(5-2\sqrt{6}) (5+2\sqrt{6} )}=\sqrt[3]{5^2-(2\sqrt{6})^2}=\\\\=\sqrt[3]{25-24} =\sqrt[3]{1} =\boxed{1}$

10) Для начала вспоминаем формулы:

$\Large \boldsymbol {} \sin \alpha \pm\beta =\sin\alpha \cos\beta \pm\cos\alpha \sin\beta \\\\\cos (\pi +\alpha ) = -\cos\alpha$

Применяем их в нашем выражении:

$\Large \boldsymbol {} 2\sin (\frac{\pi }{6} - \alpha ) + \cos (\pi +\alpha ) + \sqrt{3}\sin \alpha =2(\sin \frac{\pi }{6} \cos\alpha+\\\\+\cos \frac{\pi }{6} \sin\alpha )-\cos \alpha +\sqrt{3}\sin \alpha$

sin π/6 = 1/2; cos π/6 = √3/2. Подставляем:

$\Large \boldsymbol {} 2( \frac{1}{2} \cos\alpha- \frac{\sqrt{3} }{2} \sin\alpha )-\cos \alpha +\sqrt{3}\sin \alpha=\not2*\frac{1}{\not2} \cos\alpha-\\\\-\not2*\frac{\sqrt{3} }{\not2} \sin\alpha -\cos \alpha +\sqrt{3}\sin \alpha=\cos \alpha -\sqrt{3}\sin \alpha-\\\\-\cos \alpha +\sqrt{3}\sin \alpha=0$