ДАЮ 100 БАЛЛОВ! С РЕШЕНИЕМ.
Обчислити довжину дуги кривої.
Вычислить длину дуги кривой.
Приложения:
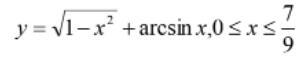
Ответы
Ответ дал:
0
Ответ:2√2/3
Пошаговое объяснение:
Приложения:
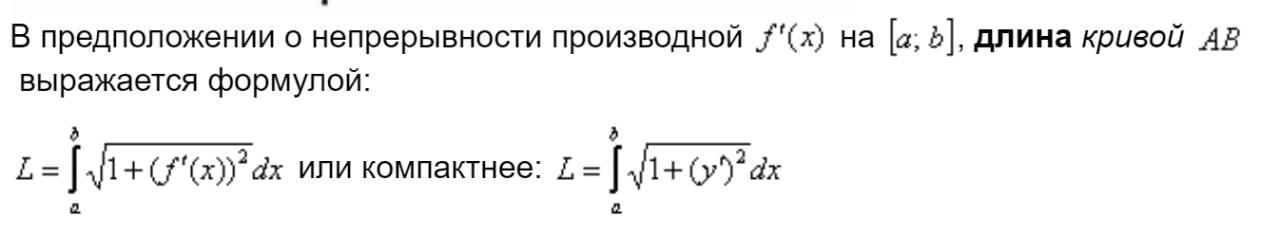
ermmak523:
Можно поэтапное решение?
Я сделал, у меня есть png картинка, но не понимаю, как её тут скинуть. Ещё недавно понял, что за вольфрам прилетают предупреждения)
отредачь просто ответ
Не знаю как, и в лс не написать
Могу тут скинуть код latex
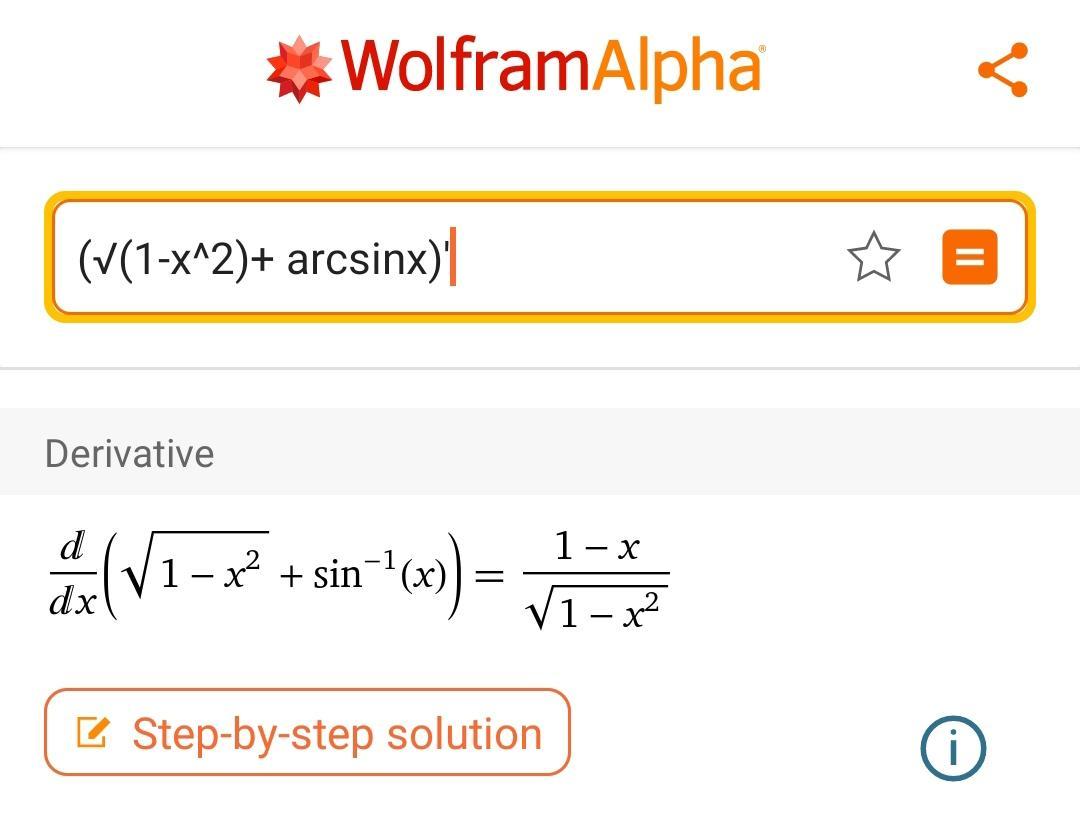
$(\sqrt{1-x^2}+\arcsin{x})'= \frac{-2x}{2\sqrt{1-x^2}}+\frac{1}{\sqrt{1-x^2}}=\frac{1-x}{\sqrt{1-x^2}}$
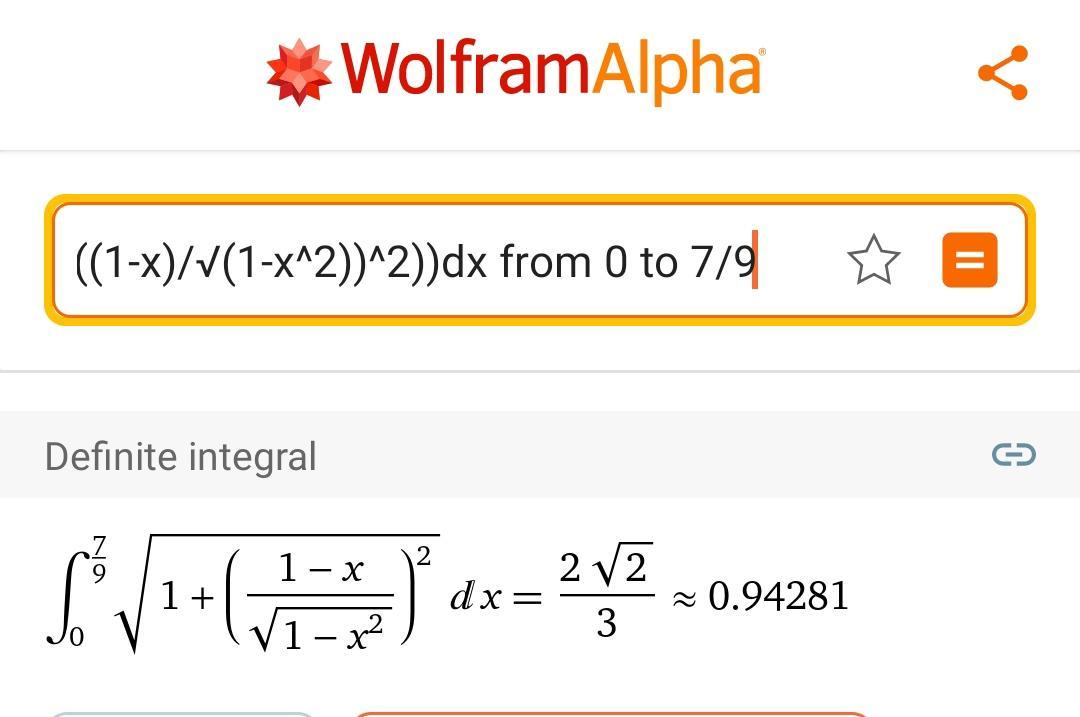
$\int\limits_0^\frac{7}{9} \sqrt{1+(\frac{1-x}{\sqrt{1-x^2}})^2} dx=\int\limits_0^\frac{7}{9} \sqrt{\frac{1-x^2}{1-x^2}+\frac{1-2x+x^2}{1-x^2}} dx =\int\limits_0^\frac{7}{9} \sqrt{\frac{2-2x}{1-x^2}} dx=\int\limits_0^\frac{7}{9} \sqrt{\frac{2(1-x)}{(1-x)(1+x)}} dx=$
$\int\limits_0^\frac{7}{9} \sqrt{1+(\frac{1-x}{\sqrt{1-x^2}})^2} dx=\int\limits_0^\frac{7}{9} \sqrt{\frac{1-x^2}{1-x^2}+\frac{1-2x+x^2}{1-x^2}} dx =\int\limits_0^\frac{7}{9} \sqrt{\frac{2-2x}{1-x^2}} dx=\int\limits_0^\frac{7}{9} \sqrt{\frac{2(1-x)}{(1-x)(1+x)}} dx=$
$=\sqrt{2}\int\limits_0^\frac{7}{9} \sqrt{\frac{1}{1+x}} dx=\sqrt{2}\int\limits_0^\frac{7}{9} {\frac{1}{\sqrt{1+x}}} dx=\sqrt{2}\int\limits_0^\frac{7}{9} {(1+x)^{-0.5}} d(1+x)=$
$=2\sqrt{2}(1+x)^{0.5}|_0^{\frac{7}{9}}=2\sqrt{2}((1+\frac{7}{9})^{0.5}-1)=2\sqrt{2}((\frac{16}{9})^{0.5}-1)=$
$=2\sqrt{2}(\frac{4}{3}-1)=\frac{2\sqrt{2}}{3}$
$=2\sqrt{2}(1+x)^{0.5}|_0^{\frac{7}{9}}=2\sqrt{2}((1+\frac{7}{9})^{0.5}-1)=2\sqrt{2}((\frac{16}{9})^{0.5}-1)=$
$=2\sqrt{2}(\frac{4}{3}-1)=\frac{2\sqrt{2}}{3}$
Можешь пожалуйста в телеге скинуть? - @mak_fgc
Вас заинтересует
2 года назад
2 года назад
2 года назад
8 лет назад
8 лет назад
9 лет назад