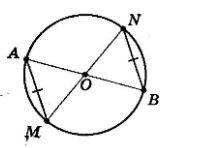
AB - діаметр кола, AM і BN - рівні хорди (див. рисунок). Доведіть, що прямі AM і BN паралельні.
Вказівка: порівняйте трикутники AOM і BON
Приложения:
Ответы
Ответ дал:
0
Ответ:
Доказано, что АМ || NB.
Объяснение:
AB-диаметр круга, AM и BN - равные хорды (см. рисунок). Докажите, что прямые AM и BN параллельны.
Дано: Окр.О;
АВ - диаметр;
AM = BN - хорды;
Доказать: AM || BN
Доказательство:
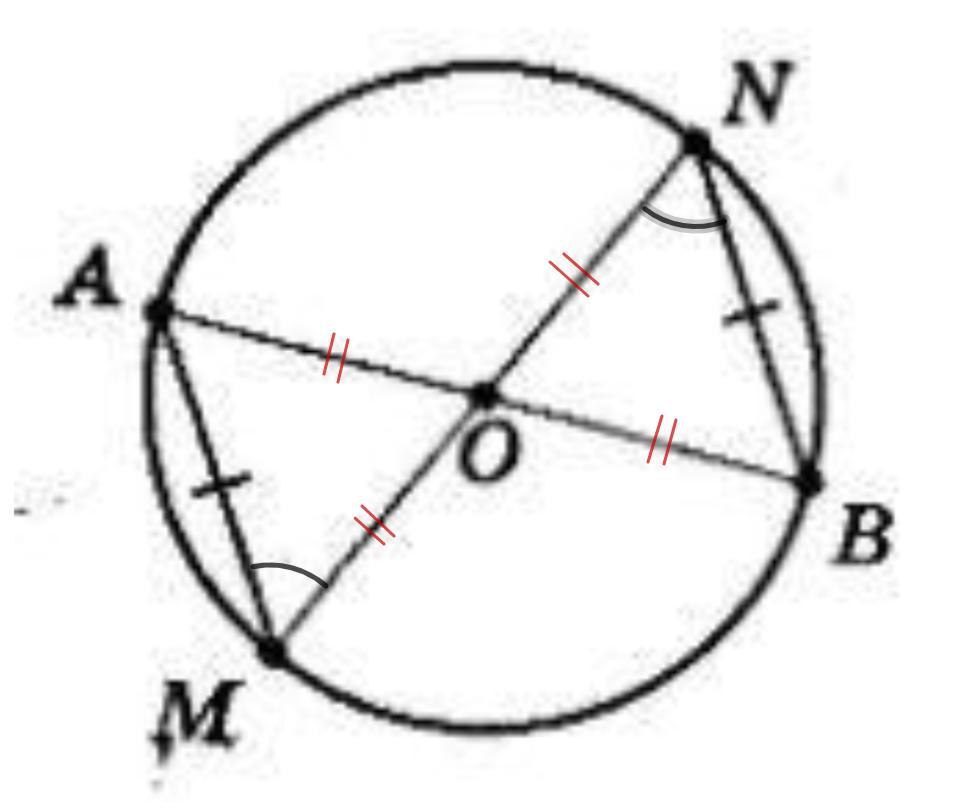
Рассмотрим ΔАОМ и ΔONB.
AM = BN (условие)
АО = ОВ = ОМ = ON - радиусы одной окружности.
⇒ ΔАОМ = ΔONB (по трем сторонам, 3 признак)
- В равных треугольниках против равных сторон лежат равные углы.
⇒ ∠М = ∠N - накрест лежащие при АМ и NB и секущей MN.
- Если при пересечении двух прямых третьей накрест лежащие углы равны, то эти прямые параллельны.
⇒ АМ || NB.
#SPJ1
Приложения:
Вас заинтересует
2 года назад
2 года назад
2 года назад
8 лет назад
9 лет назад
9 лет назад