Question

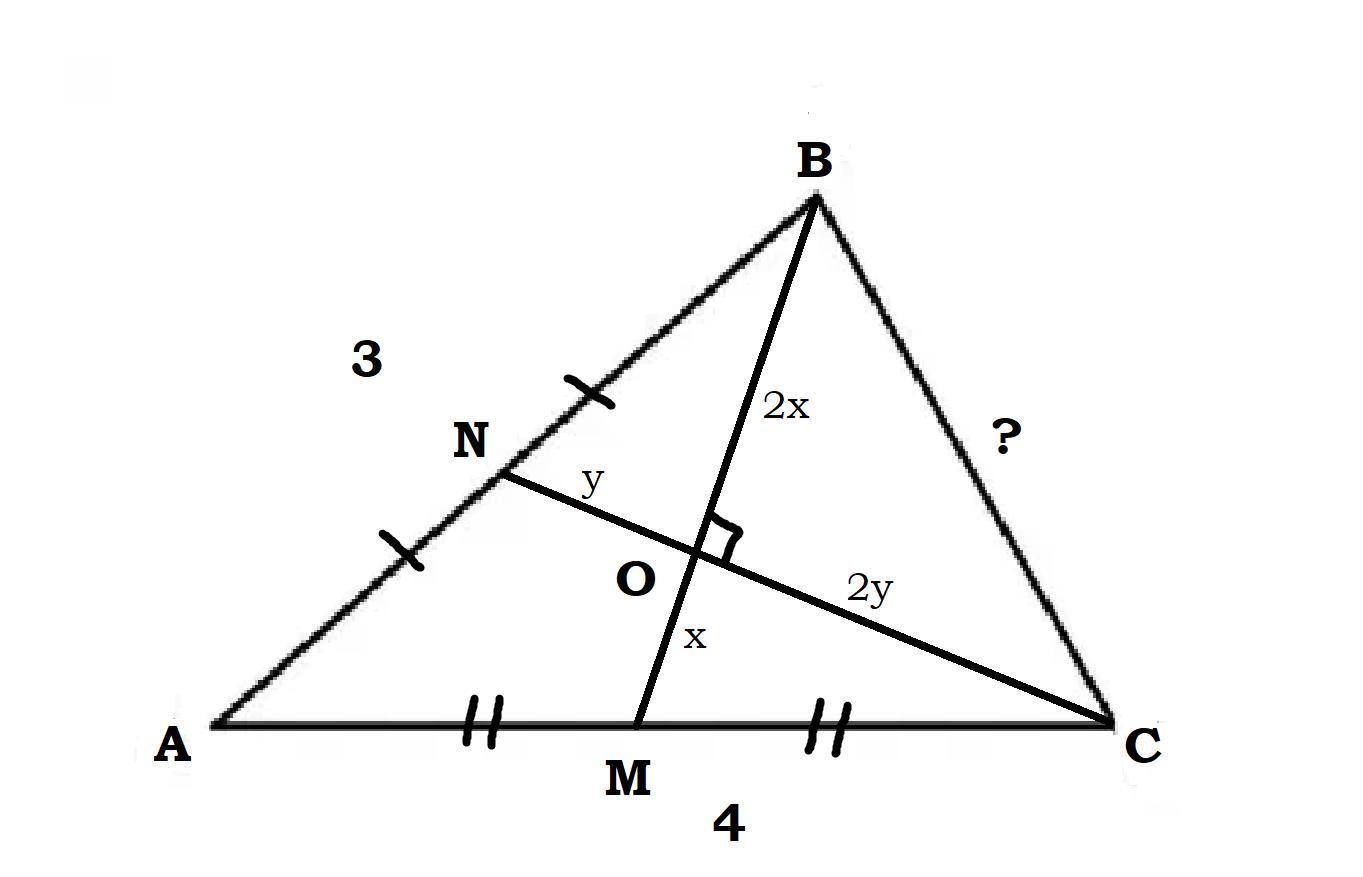
в треугольнике со сторонами 3 и 4 проведены медианы перпендикулярные друг другу. найдите третью сторону.​

Answer 1

Ответ:

третья сторона треугольника равна $\sqrt{5}$.

Объяснение:

Как я понимаю, медианы проведены к известным сторонам треугольника.

Дано:

ΔABC

AB = 3

AC = 4

BM - медиана к AC

CN - медиана к AB

BM ⋂ CN = O

∠ВОС = 90°

_________________

Найти: ВС - ?

Решение:

1) По свойству медиан треугольника, медианы пересекаются в одной точке и делятся ею в отношении 2:1, считая от вершины.

⇒ Т.е. BO:OM = 2:1, CO:ON = 2:1.

⇒ Обозначим ВО как 2х, а ОМ как х; CO как 2у, ON как у.

2) Также медиана делит противоположную сторону пополам (по определению).

⇒ АМ = МС = АС/2 = 4/2 = 2.

⇒ AN = NB = AB/2 = 3/2 = 1,5.

3) Рассмотрим ΔNOB:

• ∠NOB = 90° (по усл.)
• NO = y (см. п. 1)
• OB = 2x (см. п. 1)
• NB = 1,5 (см. п. 2)

⇒ по т. Пифагора: $NO^{2} +OB^{2} =NB^{2}$

⇒ $y^{2} +(2x)^{2} =(1,5)^{2}$

⇒ $y^{2} +4x^{2} =2,25$

4) Рассмотрим ΔМОС:

• ∠МОС = 90° (по усл.)
• ОМ = х (см. п. 1)
• ОС = 2у (см. п. 1)
• МС = 2 (см. п. 2)

⇒ по т. Пифагора: $MO^{2} +OC^{2} =MC^{2}$

⇒ $x^{2} +(2y)^{2} =2^{2}$

⇒ $x^{2} +4y^{2} = 4$

5) Из уравнений из п. 3 и п. 4 составим систему:

$\left \{ {{y^{2}+4x^{2} =2,25 } \atop {x^{2} + 4y^{2} = 4 }} \right.$

Сначала решим эту систему относительно $x^{2}$ и  $y^{2}$: выразим $y^{2}$ через $x^{2}$ в первом уравнении и подставим во второе.

$\left \{ {{y^{2} +4x^{2} =2,25} \atop {x^{2} +4y^{2}=4 }} \right. \Leftrightarrow \left \{ {{y^{2} =2,25-4x^{2} } \atop {x^{2} +4(2,25-4x^{2})=4 }} \right. \Leftrightarrow\left \{ {{y^{2} =2,25-4x^{2} } \atop {x^{2} +9-16x^{2} =4 }} \right. \Leftrightarrow \left \{{{y^{2} =2,25-4x^{2} } \atop {-15x^{2} =-5}} \right. \Leftrightarrow \left \{{{y^{2} =2,25-4*\frac{1}{3}} \atop {x^{2} =\frac{1}{3} }} \right. \Leftrightarrow \left \{{{y^{2} =\frac{11}{12} } \atop {x^{2} =\frac{1}{3} }} \right.$

Т.к. х и у выражают длины отрезков, они  не могут быть отрицательными, поэтому

$\left \{ {{y^{2}=\frac{11}{12} } \atop {x^{2} =\frac{1}{3} }} \right. \Rightarrow \left \{ {{y=\sqrt{\frac{11}{12} } } \atop {x=\sqrt{\frac{1}{3} } }} \right.$

6) Рассмотрим ΔВОС:

• ∠ВОС = 90° (по усл.)
• BO = 2x = $2\sqrt{\frac{1}{3} }$ (см. п. 1 и п. 5)
• ОС = 2у = $2\sqrt{\frac{11}{12} }$ (см. п. 1 и п. 5)

⇒ по т. Пифагора: $BO^{2} +OC^{2} =BC^{2}$

⇒  $(2\sqrt{\frac{1}{3} } )^{2} +(2\sqrt{\frac{11}{12} }) ^{2} = BC^{2}$

⇒ $BC^{2}=4*\frac{1}{3} +4*\frac{11}{12} = \frac{4}{3}+\frac{11}{3} =\frac{15}{3} = 5$

Т.к. сторона не может иметь отрицательную длину, $BC = \sqrt{5}$.

#SPJ1