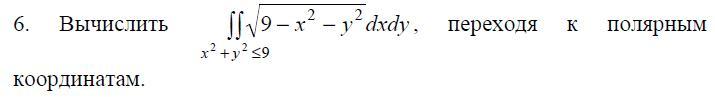Question

Задание приложено...

Answer 1

Ответ:

$\boxed{ \boldsymbol{\ \ \displaystyle \iint\limits_{x^{2} + y^{2} \leq 9} \sqrt{9 - x^{2} - y^{2}} \, dxdy = 18\pi}}$

Примечание:

$\boxed{\sin^{2}\alpha + \cos^{2} \alpha = 1}$ - основное тригонометрическое тождество

Переход от декартовых координат к полярным в двойном интеграле можно осуществить с помощью якобиана перехода.

$\boxed{ \boldsymbol{ \displaystyle \iint\limits_{G} {f(x,y)} \, dxdy = \iint\limits_{G} {f(r \cos \phi,r \sin \phi)}r \, drd\phi = \int\limits^{\beta }_{\alpha } \, d\phi \int\limits^{r_{2}(\phi)}_{r_{1}(\phi)} {r} \, dr}}$

Объяснение:

$\displaystyle \iint\limits_{x^{2} + y^{2} \leq 9} \sqrt{9 - x^{2} - y^{2}} \, dxdy = 18\pi$

Перейдем в двойном интеграле от полярных к декартовым координатам:

Переход от полярной к декартовой системе координат осуществляется по формулам:

$\displaystyle \left \{ {{x= r \cos \phi} \atop {y = r \sin \phi}} \right.$

Запишем область по которой происходит интегрирование в полярной системе координат:

$x^{2} + y^{2} \leq 9$

$(r \cos \phi)^{2} + (r \sin \phi)^{2}\leq 9$

$r^{2} \cos^{2} \phi + r^{2} \sin^{2} \phi \leq 9$

$r^{2} (\cos^{2} \phi + \sin^{2} \phi) \leq 9$

$r^{2} \leq 9$

и так как $a -$ радиус окружности, а полярный радиус $(r)$ всегда больше нуля, то $\boldsymbol{ 0\leq r \leq 3}$.

Так как интегрируем по кругу, то полярный угол будет

меняться от 0 до 2π.

(преобразование $((r \cos \phi)^{2} + (r \sin \phi)^{2}) = r^{2})$ (смотрите выше))

----------------------------------------------------------------------------------------------------------

$\displaystyle \iint\limits_{x^{2} + y^{2} \leq 9} \sqrt{9 - x^{2} - y^{2}} \, dxdy = \iint\limits_{r \leq 3} \sqrt{9 - ( r \cos \phi)^{2} - (r \sin \phi)^{2}} \, rdrd\phi =$

$\displaystyle = \iint\limits_{r \leq 3} \sqrt{9 - (( r \cos \phi)^{2} + (r \sin \phi)^{2})} \, rdrd\phi = \iint\limits_{r \leq 3} r\sqrt{9 - r^{2}} \, drd\phi =$

$\displaystyle = \int\limits^{2\pi }_{0} \, d\phi \int\limits^{3}_{0} { r\sqrt{9 - r^{2}}} \, dr =$

-----------------------------------------------------------------------------------------------------

Замена: $9 - r^{2} = t \Longrightarrow dt = d(9 - r^{2}) \ dr = -2r \ dr$

Новые границы интегрирования:

$t_{1} = 9 - r_{1}^{2} = 9 - 0^{2} = 9$

$t_{2} = 9 - r_{2}^{2} = 9 - 3^{2} = 9 - 9 = 0$

------------------------------------------------------------------------------------------------------

$\displaystyle = \int\limits^{2\pi }_{0} \, d\phi \int\limits^{3}_{0} \bigg( -\frac{1}{2} \bigg) { r\sqrt{9 - r^{2}}} \, \cdot( -2) \ dr = \int\limits^{2\pi }_{0} \, d\phi -\int\limits^{0}_{9} {\frac{\sqrt{t} }{2} } \, dt = \int\limits^{2\pi }_{0} \, d\phi \int\limits^{9}_{0} {\frac{\sqrt{t} }{2} } \, dt =$

$= \displaystyle \int\limits^{2\pi }_{0} \, d\phi \int\limits^{9}_{0} {\frac{\sqrt{t} }{2} } \, dt = \frac{1}{2} \int\limits^{2\pi }_{0} \Bigg(\sqrt[2]{t^{3}} \bigg|^{9}_{0} \Bigg) \, d\phi = \frac{1}{2} \int\limits^{2\pi }_{0} \Bigg( \frac{2}{3} \sqrt[2]{t^{3}} \bigg|^{9}_{0} \Bigg) \, d\phi =$

$\displaystyle =\frac{1}{3} \int\limits^{2\pi }_{0} \bigg( \sqrt[2]{9^{3}} - \sqrt[2]{0^{3}} \bigg) \, d\phi = \frac{1}{3} \int\limits^{2\pi }_{0} \bigg( \sqrt[2]{729} } \bigg) \, d\phi = \frac{27}{3} \cdot \phi \bigg|^{2\pi }_{0} = 9(2\pi - 0) =18\pi$.