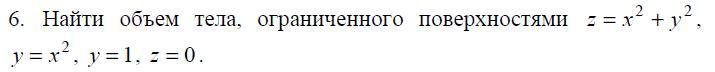Question

Вычислить с помощью двойного интеграла

Answer 1

Ответ:

$\boxed{\boldsymbol{ V = \dfrac{88}{105}}}$ кубических единиц

Примечание:

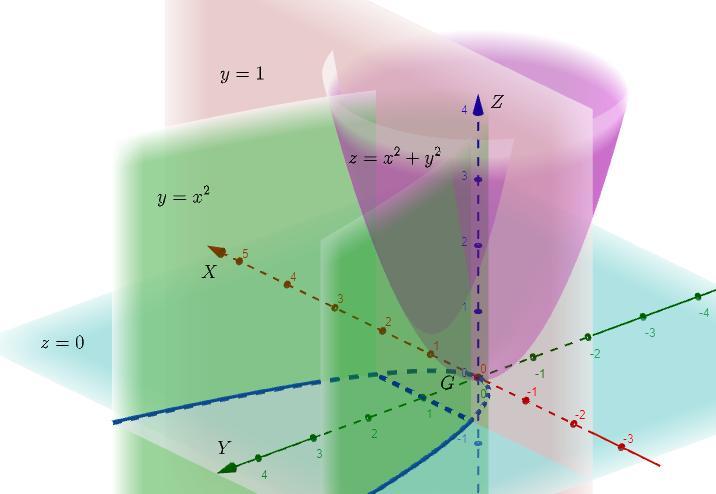
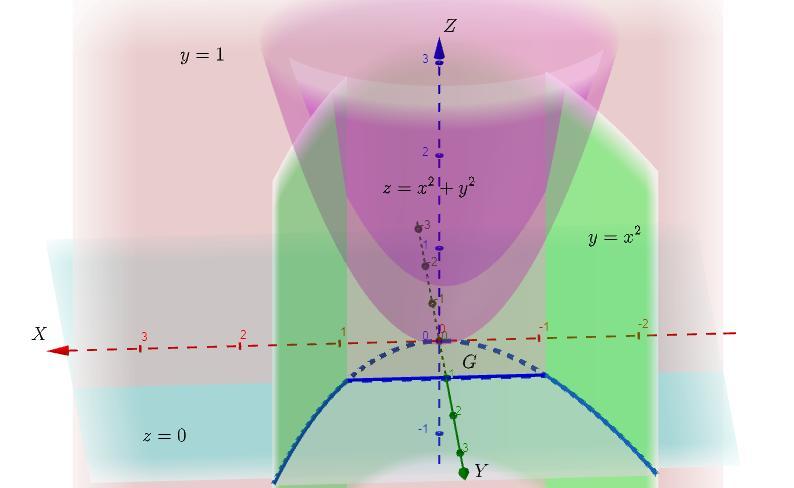
$\boxed{ \boldsymbol{ \displaystyle V = \iint\limits_{G} f(x,y) \, dxdy }}$ - объем цилиндрического тела с образующими, параллельными оси $OZ$ , ограниченное снизу областью $G$, а сверху поверхностью $z = f(x,y) \geq 0$. Данное определение показывает геометрический смысл двойного интеграла.

Для вычисления двойного интеграла сведем его к повторному интегралу. Будем интегрировать по x, поэтому приведения в общем

виде к повторному интегралу двойного по области $G$ будет в виде:

$\boxed{ \boldsymbol{ \displaystyle \iint\limits_{G} f(x,y) \, dxdy = \int\limits^a_b \, dx \int\limits^{\phi_{2}(x)}_{\phi_{1}(x)} {f(x,y)} \, dy } }$

При этом функции $\phi_{1} (x), \phi_{2} (x)$ - функции ограничивающие область $G$  снизу и сверху соответственно.

По теореме:

Если функция $y = f(x)$ непрерывна на $\mathbb R$ и является четной, то

$\boxed{ \displaystyle \int\limits^{a}_{-a} {f(x)} \, dx =2 \int\limits^a_0 {f(x)} \, dx }$ при $a > 0$.

Рассмотрим функцию $\displaystyle f(x) = \bigg( x^{2} - x^{4} - \frac{ x^{6} }{3} + \frac{1}{3} \bigg)$.

$\displaystyle f(-x) = \bigg( (-x)^{2} - (-x)^{4} - \frac{ (-x)^{6} }{3} + \frac{1}{3} \bigg) = \bigg( x^{2} - x^{4} - \frac{ x^{6} }{3} + \frac{1}{3} \bigg) = f(x)$

Так как $f(-x) = f(x)$, то по определению функция является четной.

Объяснение:

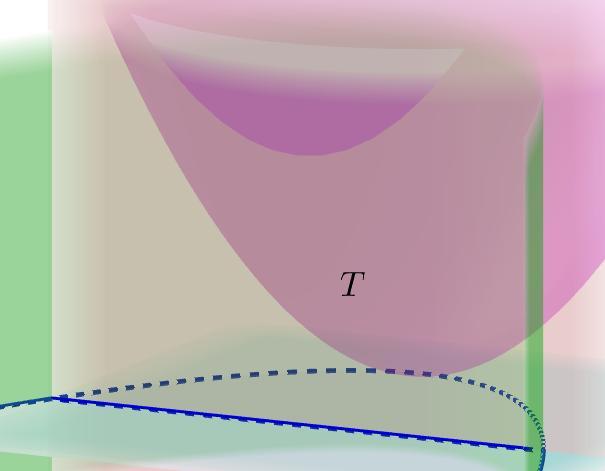
Область $T \ (XYZ)$  ограниченна поверхностями :

$z = x^{2} + y^{2}$

$z = 0$

$y = x^{2}$

$y = 1$

Снизу область ограниченна функцией $z = 0$, а сверху функцией $z = x^{2} + y^{2}$

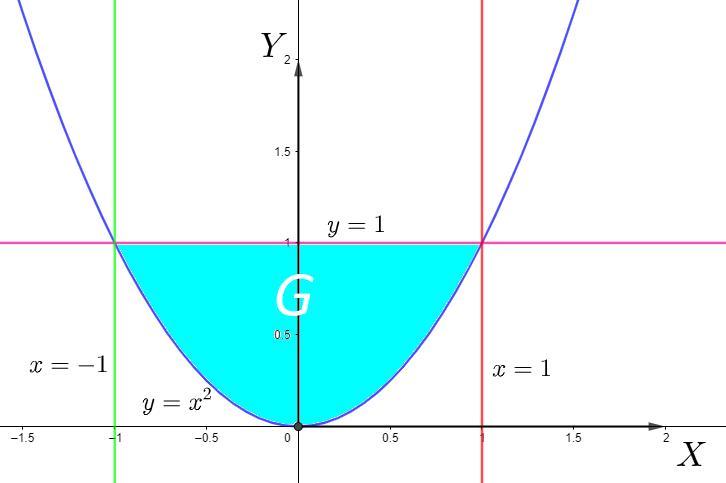
Область $G \ (XY):$

Пересечения плоскости $z = 0$ и кривой $y = x^{2}$ это кривая $\boxed{y = x^{2}}$ в плоскости $XY$.

Пересечения плоскости $z = 0$ и кривой $y = 1$ это кривая $\boxed{y = 1}$ в плоскости $XY$.

Найдем абсциссы пересечения кривой $y = x^{2}$ и $y = 1$:

$x^{2} = 1 \Longrightarrow x_{1,2} = \pm 1$

Границы интегрирования: от -1 до 1

----------------------------------------------------------------------------------------------------------

$\displaystyle V= \iint\limits_{G} (x^{2} + y^{2}) \, dxdy = \int\limits^{1}_{-1} \, dx \int\limits^{1}_{x^{2}} {(x^{2} + y^{2})} \, dy = \int\limits^{1}_{-1} \bigg( \bigg(yx^{2} + \frac{y^{3}}{3} \bigg)\bigg |^{1}_{x^{2}} \bigg) \, dx=$

$\displaystyle = \int\limits^{1}_{-1} \bigg( \bigg( 1 \cdot x^{2} + \frac{1^{3}}{3} \bigg) - \bigg( x^{2} \cdot x^{2} + \frac{(x^{2} )^{3}}{3} \bigg) \bigg) \, dx = \int\limits^{1}_{-1} \bigg( \bigg( x^{2} + \frac{1}{3} \bigg) - \bigg( x^{4} + \frac{ x^{6} }{3} \bigg) \bigg) \, dx =$

$\displaystyle = \int\limits^{1}_{-1} \bigg( x^{2} - x^{4} - \frac{ x^{6} }{3} + \frac{1}{3} \bigg) \, dx = 2\int\limits^{1}_{0} \bigg( x^{2} - x^{4} - \frac{ x^{6} }{3} + \frac{1}{3} \bigg) \, dx =$

$\displaystyle = 2 \Bigg( \bigg( \frac{x^{3}}{3} - \frac{x^{5}}{5} - \frac{x^{7}}{21} + \frac{x}{3} \bigg) \bigg |^{1}_{0} \Bigg) = 2 \Bigg( \bigg( \frac{1^{3}}{3} - \frac{1^{5}}{5} - \frac{1^{7}}{21} + \frac{1}{3} \bigg)- \bigg( \frac{0^{3}}{3} - \frac{0^{5}}{5} - \frac{0^{7}}{21} + \frac{0}{3}\bigg) \Bigg)=$

$\displaystyle = 2 \bigg( \frac{1}{3} - \frac{1}{5} - \frac{1}{21} + \frac{1}{3} \bigg) = 2 \bigg( \frac{35 - 21 - 5 + 35}{105} \bigg) = 2 \bigg( \frac{70 - 26}{105} \bigg) =\frac{2 \cdot 44}{105} = \frac{88}{105}$

кубических единиц.