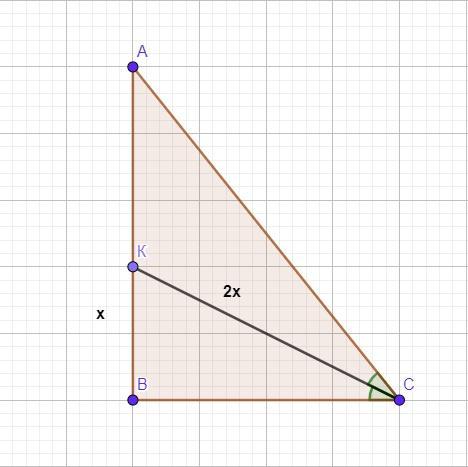
У прямокутному трикутнику ABC з гіпотенузою AC проведено бісектрису CK. Відрізок KC вдвічі більший за відрізок KB і на 12 см менший від катета AB. Знайдіть довжину катета AB.
Ответы
Ответ:
Катет АВ=36см
Объяснение:
Дано: ΔАВС(∠В=90°), КС - биссектриса (∠КСВ=∠КСА), КС=2*КВ, КС=(АВ-12) см,
Найти: АВ.
Пусть КВ= х см, тогда КС= 2х см.
В прямоугольном треугольнике КВС(∠В=90°) катет КВ в два раза меньше гипотенузы КС.
Известно, что катет прямоугольного треугольника, лежащий против угла в 30°, равен половине гипотенузы.
Следовательно ∠КСВ=∠КСА=30°, тогда ∠АСВ=2 *∠КСВ =60°, так как КС - биссектриса.
Сумма острых углов прямоугольного треугольника равна 90°, поэтому ∠ВАС=90°- ∠АСВ = 90°-60°=30°.
В ΔАКС углы при основании равны: ∠КАС=∠КСА=30°, ⇒
ΔАКС - равнобедренный.
АК=КС=2х - так как в равнобедренном треугольнике боковые стороны равны.
Итак, АВ = КС+12 = 2х+12 - по условию,
АВ = АК+КВ = 2х+х = 3х
Составим и решим уравнение:
2х+12=3х
х=12
КВ= 12 см
Катет АВ=3х=3*12= 36 см
#SPJ1