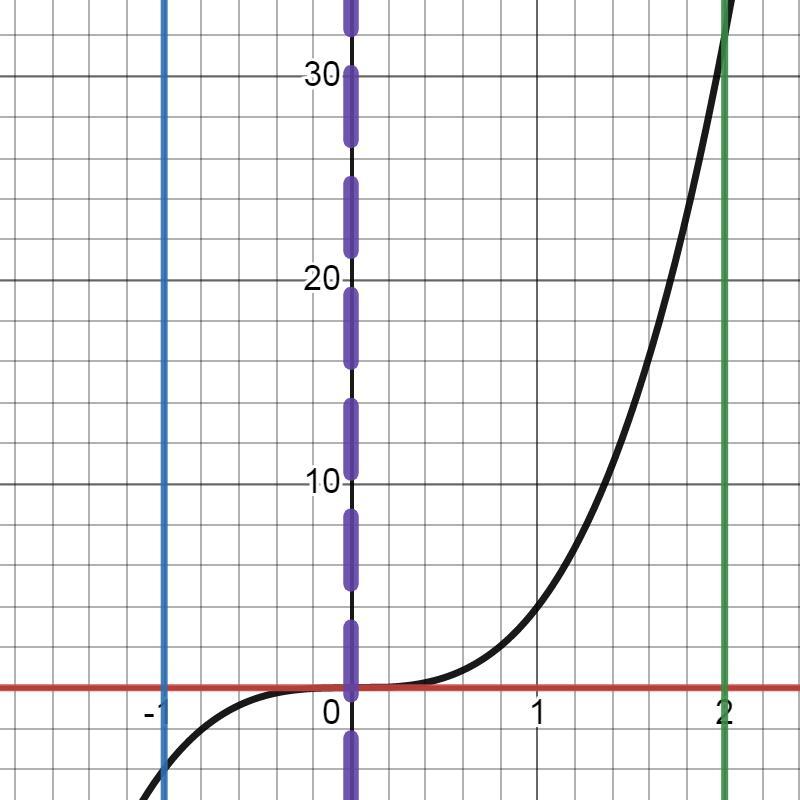
1) знайти площу фігури яка обмежена заданими лініями y=4x³; y=0 ;x=-1 ;x=2
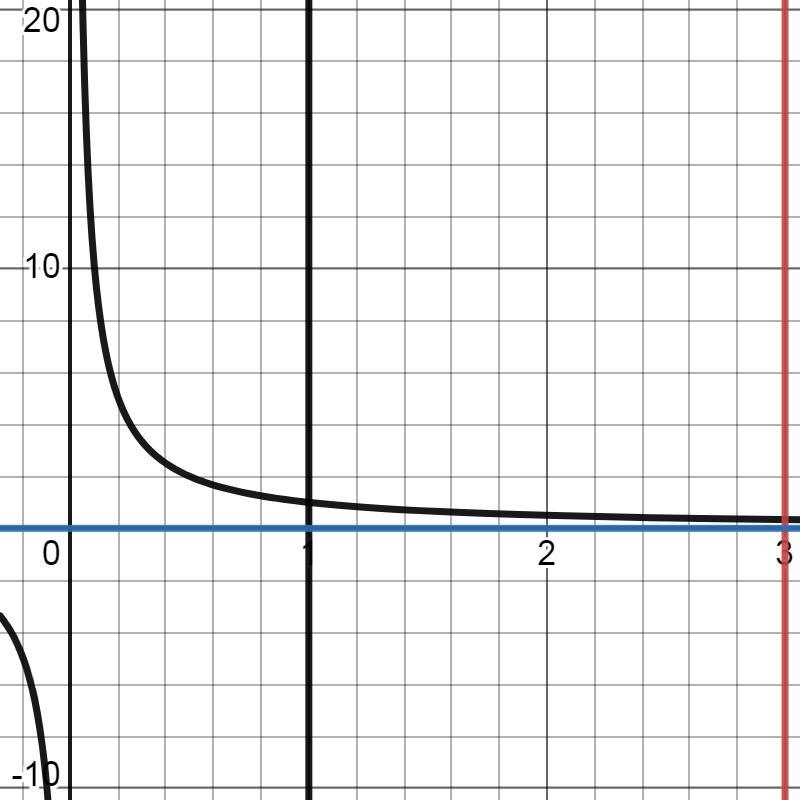
2)знайти площу фігури яка обмежена заданими лініями y=1/x; y=0;x=1; x=3
треба і з графіками і розв'язком !!!!
Ответы
Ответ дал:
0
Объяснение:
1)
Ответ: S=17 кв. ед.
2)
Ответ: S≈1,1 кв. ед.
Приложения:
sangers1959:
Я решаю дальше.
здравствуйте помогите пожалуйста решить задачу, интеграл
Вас заинтересует
2 года назад
2 года назад
2 года назад
2 года назад
7 лет назад
7 лет назад
9 лет назад