Question

ОЧЕНЬ СРОЧНО ПРОШУ!!!!!!
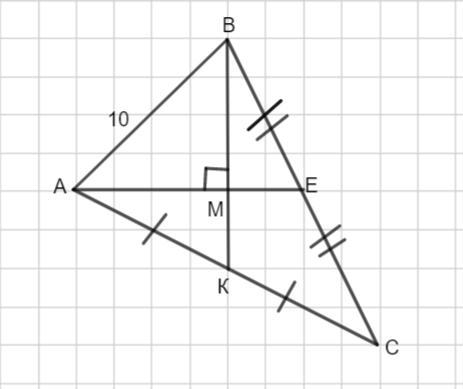
В треугольнике ABC,проведены две медианы AE и BK,которые пересекаются в точке M.AE перпендикулярно BK,BK=12,AB=10.Найдите площадь ABC.


(пожалуйста пишите полноценные решения,даю 20 баллов)

Answer 1

Ответ:

Площадь треугольника АВС равна 72 кв.ед.

Пошаговое объяснение:

В треугольнике АВС проведены медианы АЕ и ВК, которые взаимно перпендикулярны и пересекаются в точке М.

Медиана ВК =12 ед., а сторона АВ =10 ед. Надо найти площадь треугольника АВС.

Медианы треугольника пересекаясь, делятся в отношении 2: 1, считая от вершины.

Тогда, если ВК =12 ед, то КМ = 12:3=4 ед., ВМ= 8 ед.

Рассмотрим Δ АМВ. Если медианы взаимно перпендикулярны, то данный треугольник прямоугольный. Найдем катет АМ по теореме Пифагора: в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.

$AB^{2} =AM^{2} +BM^{2} ;\\AM^{2}=AB^{2} -BM^{2} ;\\AM = \sqrt{AB^{2} -BM^{2}} ;\\AM= \sqrt{10^{2} -8^{2} } =\sqrt{100-64} =\sqrt{36} =6$

Три медианы треугольника делят треугольник на 6 равновеликих треугольников, то есть 6 треугольников с равной площадью.

Тогда площадь треугольника ΔАВС в 3 раза больше площади

ΔАМВ.

Найдем площадь прямоугольного Δ АМВ, как полупроизведение катетов.

$S{_{AMB}}=\dfrac{1}{2} \cdot AM\cdot MB;\\\\S{_{AMB}}=\dfrac{1}{2} \cdot 6\cdot 8=3\cdot8=24.$

Тогда площадь ΔАВС в 3 раза больше.

$S{_{ABC}}=3\cdot 24 =72$ кв. ед.

#SPJ1