Ответы
Ответ: площадь поверхности конуса равна 36π см².
Объяснение:
Видимо, в условии ошибка - единицы измерения величин чаще всего одинаковы или близки: или см, или дм, или м, или ...
Будем считать, что все единицы измерения - см.
Площадь поверхности конуса находят по формуле
Sпов = Sбок + Sосн, где Sосн = πR², Sбок = πRL,
Sосн - площадь основания, Sбок - площадь боковой поверхности, R - радиус основания, L - образующая.
Т.е. Sпов = πR² + πRL = πR(R + L).
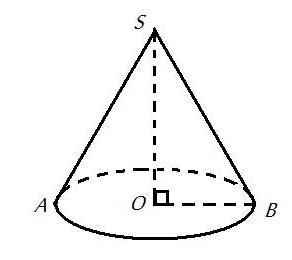
См. рисунок.
Как известно, диаметр - это хорда, проходящая через центр круга, т.е.
D = 2R. П условию D = 8 см, тогда R = D : 2 = 8 : 2 = 4 (см).
В прямоугольном ΔSOB катет ОВ = R = 4 см, высота конуса SO = 3 см, тогда по теореме Пифагора образующую L = SB можно найти так:
SB² = OB² + SO² = 4² + 3² = 16 + 9 = 25, значит, L = SВ = 5 (см).
Значит, Sпов = π · 4 · (4 + 5) = 4π · 9 = 36π (см²).
#SPJ1