Question

ПОЖАЛУЙСТА ПОМОГИТЕ НУЖНО ФОТО РЕШЕНИЯ
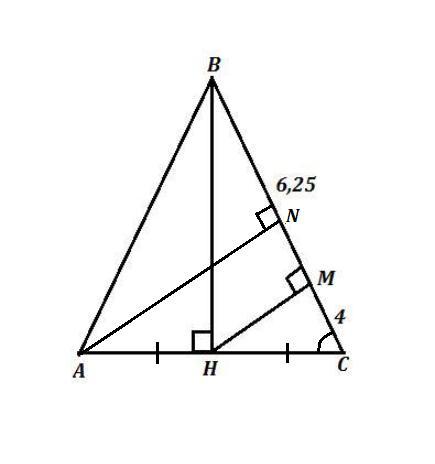
Перпендикуляр, проведений із середини основи рівнобедреного трикутника до бічної сторони, ділить її на відрізки завдовжки 4 см і 6,25 см. Знайди висоту трикутника, проведену до бічної сторони.

Answer 1

Ответ:   10 см .

ΔАВС , АВ=ВС  ⇒  ΔАВС - равнобедренный ,

точка Н - середина основания АС  ⇒   АН=СН ,  ВН - медиана,

проведённая к основанию равнобедренного треугольника ⇒

ВН является ещё и высотой , значит  ΔВНС - прямоугольный Δ и ∠ВНС=90° .

Провели  НМ ⊥ ВС , то есть НМ - высота, опущенная из прямого угла ΔВНС на гипотенузу .

Для такой высоты справедливо свойство   НМ²=ВМ·МС .

По условию ВM=6,25 см , МC=4 см .

HМ²=6,25·4=25 (см²)   ⇒   HМ=5 см .

Проведём высоту AN к боковой стороне ВС , AN ⊥ BC .

Рассмотрим ΔACN  и  ΔНСМ . Они подобны по двум углам,

∠ANC=∠HMC=90°  и  ∠С - общий .

Так как АН=СН , то АС=АН+СН=2*НС и коэффициент подобия треугольников ACN и НСМ равен 2 .  

Значит,  AN=2*HM=2*5=10 (cм)

Answer 2

Відповідь: 10 см

Пояснення: фото