Question

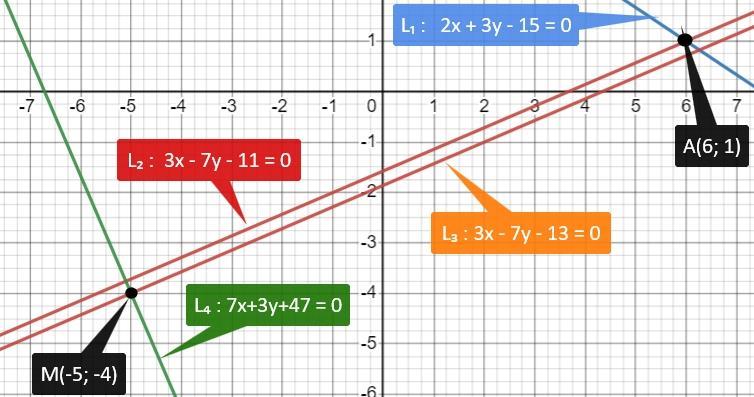
9. l1 =2x + 3y - 15 = 0
l2= 3x - 7y - 11 = 0 M(-5,-4).
Помогите пожалуйста
​

Answer 1

Ответ:

1) пересечения прямых - точка А(6; 1)

2)  уравнение прямой   L₃ : 3x - 7y - 13 = 0

3)  уравнение прямой   L₄ ; 7х + 3у + 47 = 0

4) расстояние от точки до прямой    $\displaystyle \boldsymbol { p(M,L_2)=\frac{\sqrt{58} }{29}}$

Пошаговое объяснение:

L₁ :   2x + 3y - 15 = 0

L₂ :  3x - 7y - 11 = 0

M(-5,-4)

1) точка пересечения прямых.

Надо решить систему уравнений

$\displaystyle \left \{ {{2x+3y-15=0\bigg|*\;(1.5)} \atop {3x-7y-11=0\hfill}} \right. \left \{ {{-3x-4,5y+22,5=0} \atop {3x-7y-11=0\hfill}} \right. \bigg|+\\\\\\-3x-4,5y+22,5+3x-7y-11=0\\\\-11,5y+11,5=0\\\\\underline {y=1}\\3x-7*1-11=0\\3x -18=0\\\underline {x=6}$

Таким образом, точка пересечения прямых - точка А(6; 1)

2)  L₃  ║ L₂ и  L₃  проходит через точку M(-5,-4).

Поскольку  L₃  ║ L₂ , векторы их нормалей одинаковы.

Следовательно, прямая  L₃ иммет вид

3x - 7y + С = 0

Чтобы определить свободный член С, подставим в уравнение координаты точки M(-5,-4).

3*(-5) - 7*(-4) + С = 0

15 +28 + С = 0  

С = -13.

Мы получили уравнение искомой прямой L₃ : 3x - 7y - 13 = 0 .

3) L₄  ⊥  L₂ и L₄ проходит через точку M(-5,-4).

Поскольку прямые перпендикулярны нормальный вектор  L₂  $\displaystyle \large \boldsymbol {\vec n_L_2}$ = {3; -7}  равен направляющему вектору  L₄   $\displaystyle \large \boldsymbol {\vec a_L_4}$.

Уравнение прямой через точку М с направляющим векторм  $\displaystyle \large \boldsymbol {\vec a_L_4}$ имеет вид

$\displaystyle \frac{x-x_M}{(\vec a_L_4)_x} =\frac{y-y_M}{(\vec a_L_4)_y}$

Подставим наши данные

$\displaystyle \frac{x-(-5)}{3} =\frac{y-(-4)}{-7} \\\\\\-7x-35=3y+12\\\\\underline {L_4\; :\;7x+3y+47=0}$  - это и есть уравнение искомой прямой

4) Расстояние от точки М(-5; -4) до прямой L₂ :  3x - 7y - 11 = 0

Расстояние от точки М(х; у) до прямой Ах + Ву + С = 0 рассчитывается по формуле  

$\displaystyle p(M,L_2)=\frac{|A*M_x+B*M_y+C|}{\sqrt{A^2+B^2} }$

Подставим наши данные

$\displaystyle p(M,L_2)=\frac{\bigg|3*(-5) + (-7)*(-4) + (-11)\bigg|}{\sqrt{3^2 + (-7)^2} }=\frac{2}{\sqrt{58} }=\frac{\sqrt{58} }{29}$

#SPJ1