Question

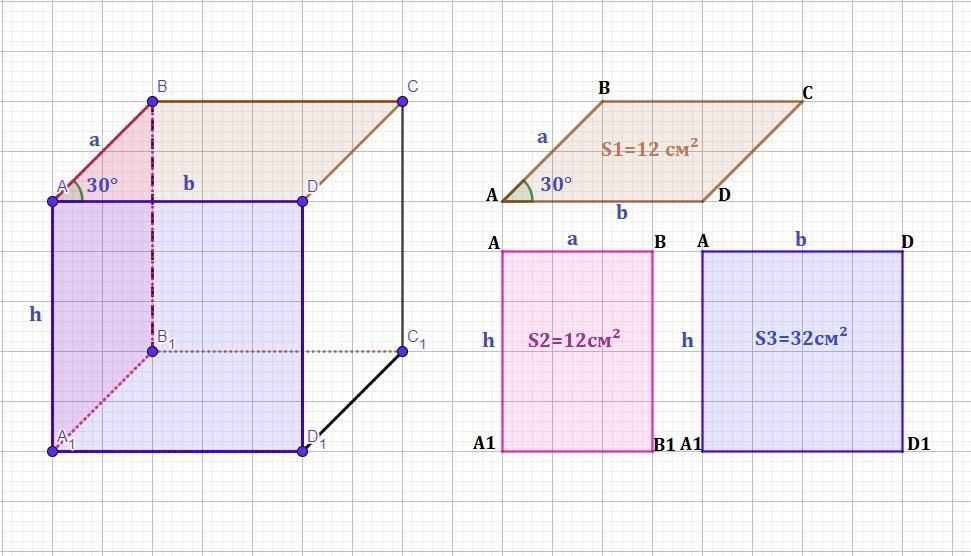
В основі прямоï призми лежить паралелограм, кут між сторонами якого дорівнює 30°. Площа
основи призми дорівнює 12 см², а площі двох бічних граней дорiвнюють 12см²
і 32см². Знайдіть висоту призми (у см).​

Answer 1

Ответ:

Висота призми = 4 см

Объяснение:

В основі прямоï призми лежить паралелограм, кут між сторонами якого дорівнює 30°. Площа основи призми дорівнює 12 см², а площі двох бічних граней дорiвнюють 12см²і 32см². Треба знайти висоту призми

• Пряма призма — це призма, у якої бічні ребра перпендикулярні до площини основи, звідки випливає, що всі бічні грані є прямокутниками.

1) Розглянемо основу призми ABCD.

За умовою ABCD - паралелограм. Хай АВ=а, AD=b, ∠BAD=30°.

Tоді площа паралелограма:

S₁ = a*b*sin∠BAD.

S₁ = 12 см² - за умовою.

a*b*sin30°=12

a*b* 1/2 = 12

a*b = 24  

⇒ b = 24/а (1)

2) Розглянемо бічну грань АВВ₁А₁.

АВВ₁А₁ - прямокутник. АВ=а, АА₁=h.

Площа прямокутника АВВ₁А₁:

S₂ = a*h

S₂ = 12 см² - за умовою.

⇒ a*h=12

h=12/a  (2)

3) Розглянемо бічну грань АDD₁А₁.

АDD₁А₁ - прямокутник. АD=b, АА₁=h.

Площа прямокутника АDD₁А₁:

S₃ = b*h

S₃ = 32 см² - за умовою.

⇒ b*h= 32

h=32/b (3)

Підставимо в (3) значення (1):

$h=\dfrac{32}{b} =\dfrac{32}{\frac{24}{a} } =\dfrac{32a}{24} =\dfrac{4a}{3}$   (4)

4) Прирівнюємо (2) і (4), знайдемо а:

$\dfrac{12}{a} =\dfrac{4a}{3}$

4a²=36

a² =9

a = 3 cм

5) Знаходимо висоту призми з (2):

h= 12/а = 12/3 = 4 см

# SPJ1