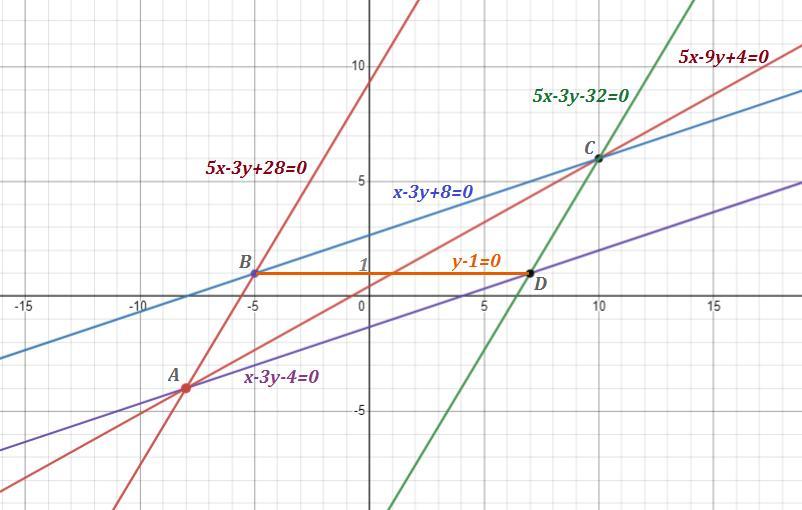
Дві сторони, які виходять з однієї вершини паралелограма, задано відповідно рівняннями 5х – 3у + 28 =0, х – 3у – 4 = 0; координати протилежної вершини паралелограма (10;6). Складіть рівняння двох інших сторін паралелограма та його
діагоналей
Ответы
Ответ дал:
0
Решение.
Пусть заданные прямые и
выходят из вершины А .
Вершина С имеет координаты С(10:6) . Она принадлежит прямым,
параллельным указанным выше прямым и
.
Составим их уравнения.
Подставим координаты точки С в уравнение .
Уравнение .
Подставим координаты точки С в уравнение .
Уравнение .
Уравнение диагонали АС составим как уравнение прямой, проходящей через две точки . Координаты точки А найдём как точку пересечения прямых и
.
Диагональ ВD проходит через точку В - точку пересечения , и точку D - точку пересечения
.
Ответ:
Приложения:
Вас заинтересует
2 года назад
2 года назад
2 года назад
7 лет назад