1. Какое из следующих выражений позволяет найти объём конуса?
1) r²h; 2) url; 3) лг² + 2нги; 4)2лгр.

2. Найдите площадь полной поверхности цилиндра с радиусом основания, равным 4 см, и выстой, равной 5 см.

3. Диаметр сечения шара плоскостью равен 24 см. Расстояние от центра шара до плоскости сечения равно 9 см. Найдите объём шара.

4. Дана правильная четырёхугольная пирамида. Площадь основания пирамиды равна 36 см2, площадь боковой поверхности- 48 см². Найдите высоту пирамиды.

5. В основании параллелепипеда лежит квадрат со стороной 4 см, боковое ребро равно 6√2 см и образует с двумя смежными рёбрами углы по 60º. Найдите обьём параллелепипеда

zmeura1204: 1) πr²h/3

Ответы

Ответ дал: dyexfnf

Ответ:

Объяснение:

№1

V = 1/3 πr²h

№2

Дано: h = 5 см; r= 4 см

Найти: Sп.п.- ?

Площадь основания равна :

Sосн. = 2πr² = 2π * 4² = 32π см²

Площадь боковой поверхности равна:

Sб.п. = 2πrh = 2π * 4 * 5 = 40π см²

Площадь полной поверхности равна:

Sп.п. = Sб.п. + Sосн. = 32π + 40π = 72π см²

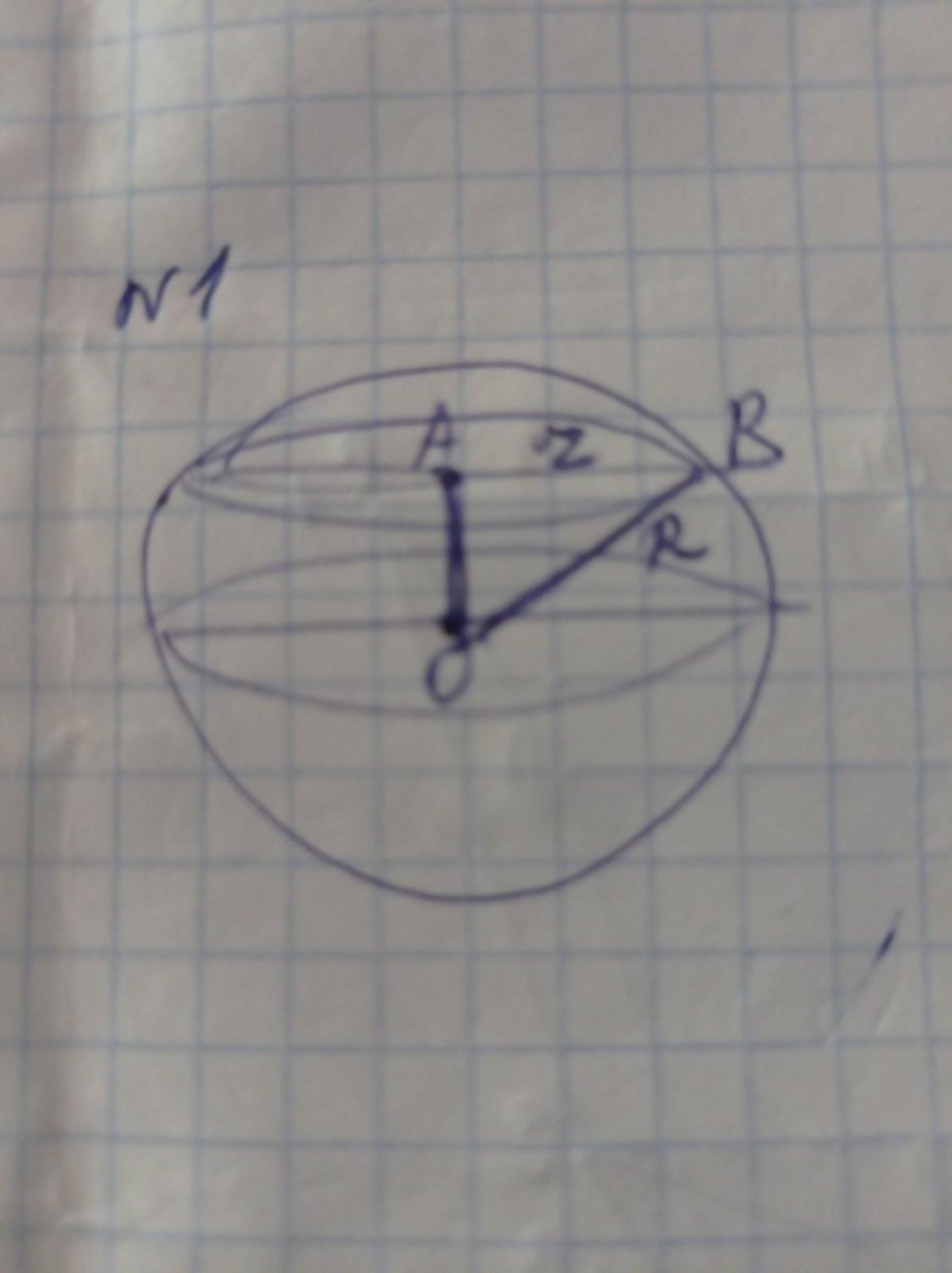
№3

Дано: h= ОА = 9 см; r = d/2 = 24/2 = 12 см

Найти: V- ?

сечение шара этот круг с радиусом r = AВ = 12cм и отсюда получаем равнобедренный треугольник АОВ, согласно т. Пифагора найдем катет ОВ, являющийся радиусом круга с центром О

R =√r² + h²=√12² + 9² = √144 + 81 = √225 = 15 см

Объём шара равен:

V = 4/3π * R³ = 4/3π * 15³ = 4500π см³

фото 1

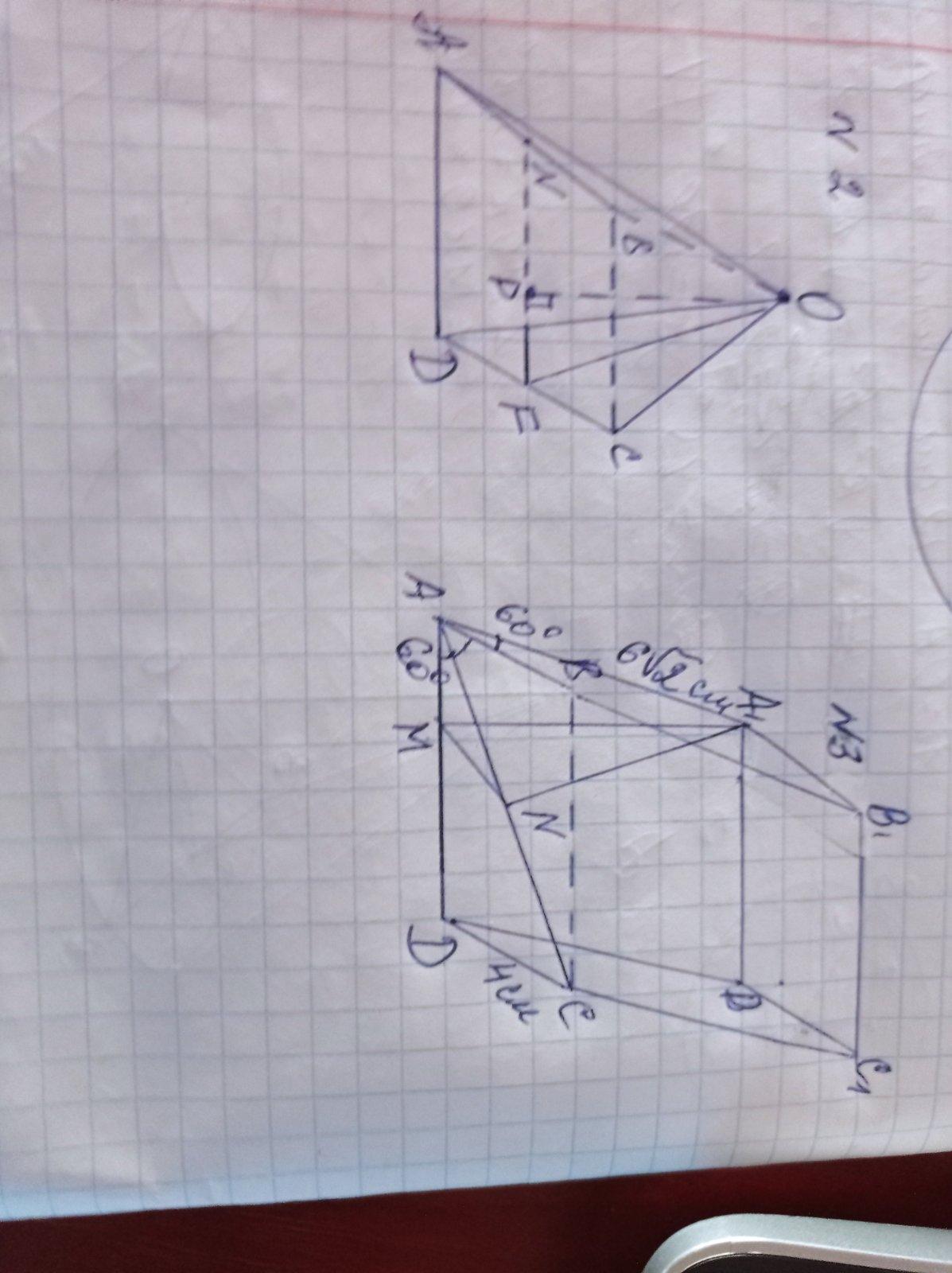
№4

Дано: Sосн. - 36см² ; Sб.п. = 48 см²

Найти: h - ?

В правильной четырёхугольной пирамиде основанием есть квадрат. В правильной пирамиде высота проходит через центр основания. Для квадрата это точка пересечения диагоналей, при этом ОР - высота пирамиды, а ОF является апофемой.

Найдем сторону квадрата из формулы площади:

S = a²

а = √36 = 6 см

Площадь грани равна S(грани) = Sб.п./n = 48 : 4 = 12 см²

Площадь Δ COD равна : S = 1/2a * h отсюда найдем высоту

h = S/(1/2а) = 12 / (1/2 * 6) = 12 : 3 = 4 см

В основании проведем прямую, делящую его пополам

РF = 6 : 2 = 3 см

Найдем высоту пирамиды согласно т. Пифагора

h =√(4²- 3²) = √(16 - 9) = √7 ≈ 2,64 см

фото 2

№5