Question

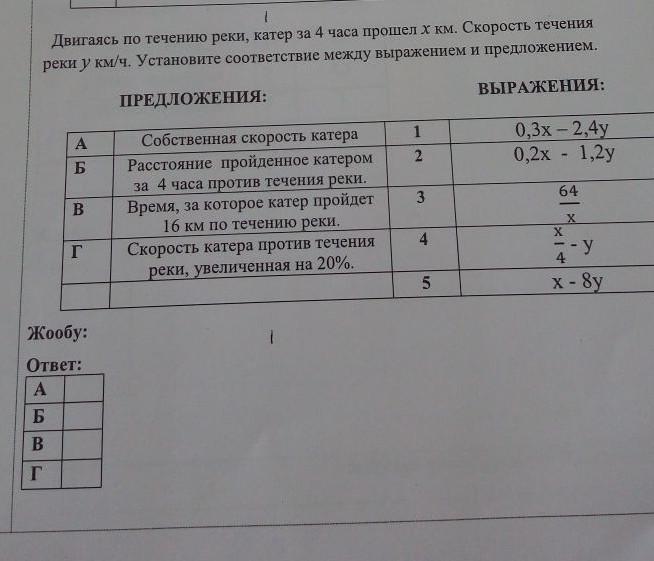
Двигаясь по течению реки, катер за 4 часа прошел х км. Скорость течения реки у км/ч. Установите соответствие между выражением и предложением.​

Answer 1

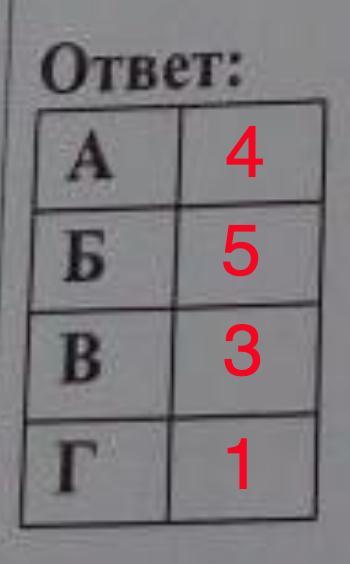
Ответ:

А. Собственная скорость катера равна $\displaystyle \left( \frac{x}{4}-y\right)$ км/ч. → ответ 4.

Б. Расстояние, пройденное катером за 4 часа против течения реки равно (х - 8у) км. → ответ 5.

В. Время, за которое катер пройдет 16 км по течению реки равно $\displaystyle \frac{64}{x}$ ч. → ответ 3.

Г. Скорость катера против течения реки, увеличенная на 20% равна  (0,3х - 2,4у) км/ч. → ответ 1.

Пошаговое объяснение:

Двигаясь по течению реки, катер за 4 часа прошел х км. Скорость течения реки у км/ч. Установите соответствие между выражением и предложением.​

Пусть собственная скорость лодки V км/ч.

Тогда скорость по течению будет равна сумме собственной скорости и скорости течения реки, то есть:

V по теч. = (V + y) км/ч

А скорость против течения будет равна разности собственной скорости и скорости течения реки, то есть:

V пр.теч. = (V - y) км/ч

Также вспомним формулы расстояния и времени:

$\displaystyle \boxed {S=Vt},\;\;\;\;\;\boxed {t=\frac{S}{V} }$.

A. Собственная скорость катера.

Двигаясь по течению реки, катер за 4 часа прошел х км. Скорость течения реки у км/ч.

Скорость по течению равна (V + y) км/ч; время 4 ч, расстояние х км.

х = (V + y) · 4   |:4

$\displaystyle \frac{x}{4}=V+y \\\\V=\frac{x}{4}-y$

Собственная скорость катера равна $\displaystyle \left( \frac{x}{4}-y\right)$ км/ч. → ответ 4.

Б. Расстояние, пройденное катером за 4 часа против течения реки.

Выразим скорость против течения реки (V пр.теч.):

$\displaystyle V-y=\left(\frac{x}{4} -y\right)-y=(0,25x-2y)$  (км/ч)

За 4 часа катер против течения пройдет:

(0,25х - 2у) · 4 = (х - 8у) (км)

Расстояние, пройденное катером за 4 часа против течения реки равно (х - 8у) км. → ответ 5.

В. Время, за которое катер пройдет 16 км по течению реки.

Скорость по течению (V по теч.) равна:

$\displaystyle V+y=\left(\frac{x}{4}-y\right)+y=\frac{x}{4}$  км/ч

Расстояние 16 км.

Найдем время:

$\displaystyle t = \frac{16}{\frac{x}{4} } =\frac{64}{x}$ (ч)

Время, за которое катер пройдет 16 км по течению реки равно $\displaystyle \frac{64}{x}$ ч. → ответ 3.

Г. Скорость катера против течения реки, увеличенная на 20%.

Первоначальная скорость против течения (0,25х - 2у) км/ч примем за 100%.

Увеличилась на 20%, значит стала 120%.

Переведем 120% в десятичную дробь, разделив данные проценты на 100:

120% это 1,2.

• Часть от числа находим умножением:

V увел. =  (0,25х - 2у) · 1,2 = (0,3х - 2,4у) (км/ч)

Скорость катера против течения реки, увеличенная на 20% равна  (0,3х - 2,4у) км/ч. → ответ 1.

#SPJ1