Question

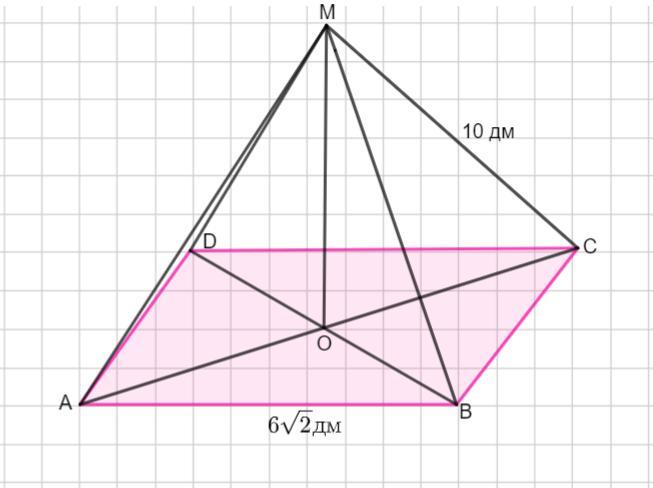
Точка М віддалена від кожної вершини квадрата на 10 дм.Знайти відстань від точки М до площини квадрата, якщо його сторона дорівнює 6 корінь квадратний з 2

Answer 1

Ответ:

Расстояние от точки М до плоскости квадрата равно 8 дм.

Объяснение:

Точка М удалена от каждой вершины квадрата на 10 дм. Найти расстояние от точки М до плоскости квадрата, если сторона квадрата равна 6√2 дм.

Пусть АВСD - квадрат. По условию АМ=ВМ=СМ=МD =10 дм.

Если точка М равноудалена от всех вершин квадрата, то она проектируется в точку  О - точку пересечения диагоналей квадрата.

( ΔМОА=ΔМОВ=ΔМОС=ΔМО по гипотенузе и общему катету МО, из равенства треугольников следует, что АО=ВО=СО=ВО)

МО - перпендикуляр к плоскости квадрата. Длина этого перпендикуляра и будет расстоянием от точки М до плоскости квадрата.  

Диагональ квадрата определяется по формуле

$d=a\sqrt{2} ,$

d- диагональ квадрата

a- сторона квадрата.

Тогда

$AC=BD= 6\sqrt{2} \cdot\sqrt{2} =6\cdot2=12$ дм.

$AO=OC=12:2=6$ дм.

Рассмотрим ΔМОС - прямоугольный.

По теореме Пифагора: в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.$MC^{2} =MO^{2} +OC^{2} ;\\MO^{2} =MC^{2}-OC^{2};\\MO= \sqrt{MC^{2}-OC^{2}} ;\\MO=\sqrt{10^{2} -6^{2} } =\sqrt{100-36} =\sqrt{64} =8$

Значит, расстояние от точки М до плоскости квадрата равно 8 дм.

#SPJ1