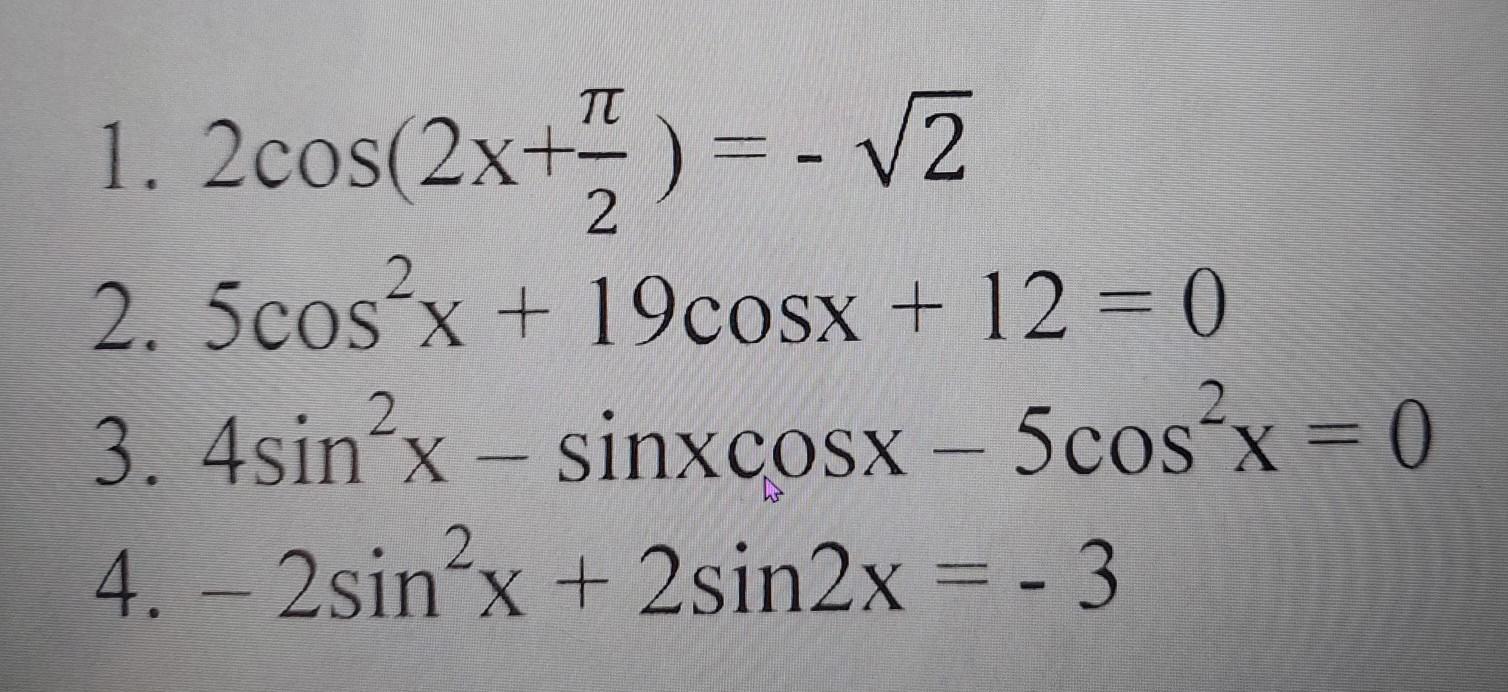Question

Помогите решить тригонометрические уравнения​

Answer 1

Ответ:

Объяснение:

  1 )  2cos( 2x + π/2 ) = - √2 ;

       cos( 2x + π/2 ) = - √2/2 ;

       2x + π/2 = ± arccos( - √2/2 ) + 2πn , nЄ Z ;

       2x + π/2 = ± ( π - arccos(√2/2 ) ) + 2πn ;

        2x = - π/2 ± 3π/4 + 2πn ;

          x = - π/4 ± 3π/8 + πn ,  nЄ Z . -  Це відповідь .

   3 ) 4sіn²x - sinxcosx - 5cos²x = 0 ;│: cos²x ≠ 0

       4sіn²x/cos²x - sinxcosx/cos²x - 5cos²x/cos²x = 0 ;  

       4tg²x - tgx - 5 = 0 ;      заміна  y = tgx

       4y² - y - 5 = 0 ;     D = 81 > 0 ;  y₁ = - 1 ;    y₂ = 1,25 .

    Повертаємося до змінної  х ;

     tgx = - 1 ;                   або           tgx = 1,25 ;

  x = - π/4 + πn ,  nЄ Z ;                     x = arctg1,25 + πn ,  nЄ Z .

#  Інші приклади - аналогічно .