Question

ПОМОГИТЕ
Рассмотрим все параллелограммы ABCD с фиксированным углом
ABC=ϕ и фиксированным периметром 2p. Для какого из этих

параллелограммов площадь будет максимальной?
Доказать

Answer 1

Ответ:

Наибольшую площадь имеет ромб со стороной $\dfrac{p}{2}$

Пошаговое объяснение:

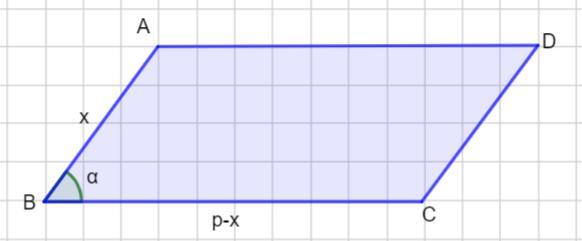
Рассмотрим параллелограмм ABCD

∠ABC = α, периметр данного параллелограмма равен 2р. Надо определить для какого параллелограмма площадь будет максимальной.

У параллелограмма противолежащие стороны равны. Поэтому сумму соседних сторон будет равна полупериметру.

Значит, AB +AD =р.

Пусть АВ = х ед. Тогда AD=(р-х) ед. Рассмотрим функцию выражающую площадь параллелограмма.

Площадь параллелограмма можно найти как произведение двух соседних сторон параллелограмма на синус угла между ними.

Значит, получим функцию

$S (x) =x\cdot (p-x) \cdot sin\alpha ;\\S(x)= (px-x^{2} )\cdot sin \alpha$

Найдем в каком случае будет  наибольшее значение данной функции.

Для этого найдем производную данной функции

$S'(x)= (p-2x)\cdot sin\alpha$

Найдем критические точки, решив уравнение:

$S'(x)=0;\\ (p-2x)\cdot sin\alpha =0;\\p-2x=0;\\2x=p;\\\\x=\dfrac{p}{2}$

Определим какая это точка. Если производная при переходе через данную точку меняет свой знак с "+" на "-" , то данная точка является точкой максимума.

Определим знак производной

$S'\left(\dfrac{p}{4}\right )= \left(p-2\cdot\dfrac{p}{4}\ight)\cdot sin\alpha=\left(p-\dfrac{p}{2}\right)\cdot sin\alpha=\dfrac{p}{2}\cdot sin\alpha > 0;$

$S'\left(\dfrac{3p}{4}\right )= \left(p-2\cdot\dfrac{3p}{4}\ight)\cdot sin\alpha=\left(p-\dfrac{3p}{2}\right)\cdot sin\alpha=-\dfrac{p}{2}\cdot sin\alpha < 0$

Так как точка $x=\dfrac{p}{2}$ единственная точка максимума, то в ней и достигается наибольшее значение .

Значит $AB =\dfrac{p}{2}$

$AD =p- \dfrac{p}{2} =\dfrac{p}{2}$

Значит, наибольшую площадь имеет ромб со стороной $\dfrac{p}{2}$

#SPJ1