Question

Обчислити площу фігури обмеженої лініями: y=1/4 (x+3)^2, 2x+4y+3=0

Answer 1

Ответ:

$\displaystyle y=\frac{1}{4}(x+3)^2;\;\;\;\;\;2x+4y+3=0$   равна $\displaystyle 2\frac{2}{3}$  ед.²

Объяснение:

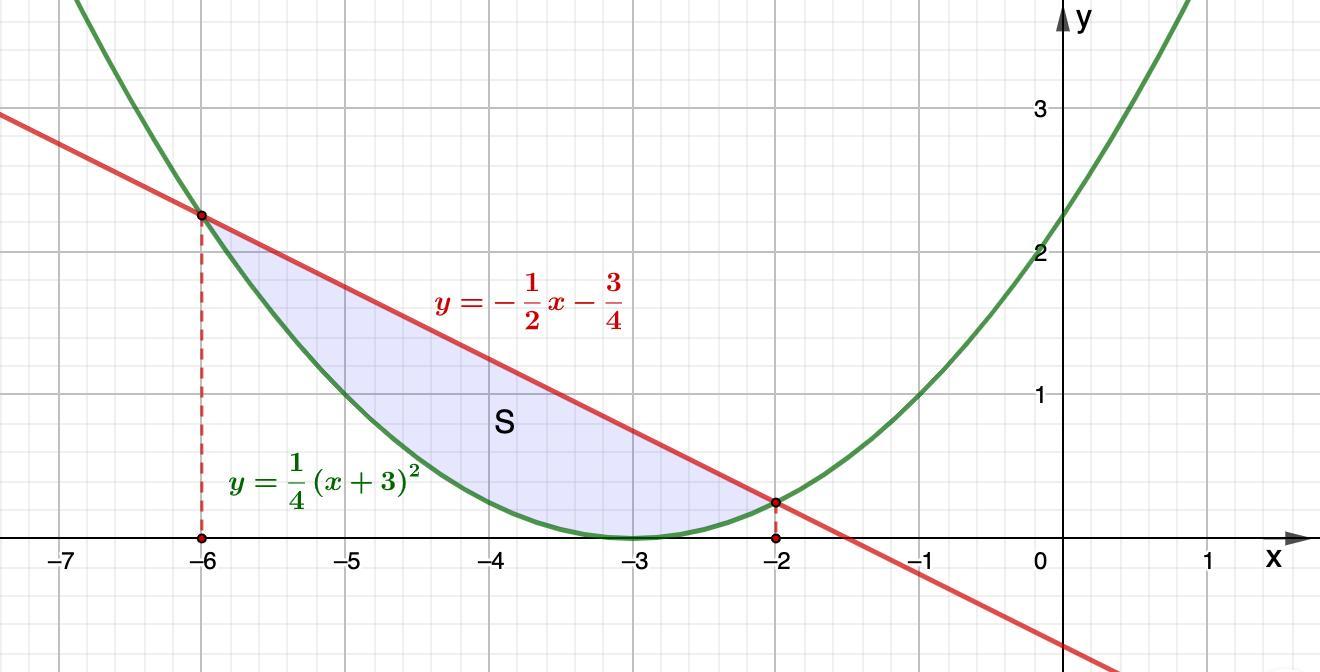
Вычислить площадь фигуры, ограниченной линиями:

$\displaystyle y=\frac{1}{4}(x+3)^2;\;\;\;\;\;2x+4y+3=0$

Выразим у из второго уравнения:

$\displaystyle y=-\frac{2x+3}{4}=-\frac{1}{2}x-\frac{3}{4}$

Определим фигуру, площадь которой надо найти.

Начертим графики:

1)

$\displaystyle y=\frac{1}{4}(x+3)^2$

-квадратичная функция, график - парабола, ветви вверх.

2)

$\displaystyle y=-\frac{1}{2}x-\frac{3}{4}$

-линейная функция график прямая.

Найдем абсциссы точек пересечения графиков. Для этого решим систему:

$\displaystyle \left \{ {{y=\frac{1}{4}(x+3)^2 } \atop {y=-\frac{1}{2}x-\frac{3}{4} }} \right. \\\\\frac{1}{4}(x^2+6x+9)=-\frac{1}{2}x-\frac{3}{4}\;\;\;|\cdot4\\ \\ x^2+6x+9=-2x-3\\ \\x^2+8x+12=0\\\\x_{1,2}=\frac{-8\pm\sqrt{64-48} }{2}=\frac{-8\pm4}{2} \\\\x_1=-2;\;\;\;\;\;x_2=-6$

Площадь фигуры найдем по формуле:

$\displaystyle \boxed { S= \int\limits^b_a {(f_2(x)-f_1(x))} \, dx }$

Так же нам понадобится формула Ньютона-Лейбница:

$\boxed {\int\limits^b_a {f(x)\, dx }=F(b)-F(a)}$

У нас: b = -2; a = -6;

$\displaystyle f_2(x)=-\frac{1}{2}x-\frac{3}{4};\;\;\;f_1(x)=\frac{1}{4}x^2+\frac{6}{4}x+\frac{9}{4}$

Найдем площадь:

$\displaystyle S=\int\limits^{-2}_{-6} {\left(-\frac{1}{2}x-\frac{3}{4}-\frac{1}{4}x^2-\frac{6}{4}x-\frac{9}{4}\right) } \, dx =\\\\=\int\limits^{-2}_{-6} {\left(-\frac{1}{4}x^2-\frac{8}{4}x-\frac{12}{4}\right) } \, dx=\\\\=-\frac{1}{4}\int\limits^{-2}_{-6} {(x^2+8x+12)} \, dx =\\\\-\frac{1}{4} \left(\frac{x^3}{3}+8\cdot\frac{x^2}{2}+12x\right)\bigg|^{-2} _{-6}=\\ \\=-\frac{1}{4} \left(-\frac{8}{3} +16-24+\frac{216}{3}-144+72\right)=$

$\displaystyle =-\frac{1}{4}\cdot\left(-\frac{32}{3}\right) =\frac{8}{3}=2\frac{2}{3}$

Площадь фигуры, ограниченной линиями:

$\displaystyle y=\frac{1}{4}(x+3)^2;\;\;\;\;\;2x+4y+3=0$   равна $\displaystyle 2\frac{2}{3}$  ед.²

#SPJ1