Question

40 баллов! В правильной шестиугольной пирамиде сторона основания равна 6 дм, высота 3 дм. Найдите площадь боковой поверхности пирамиды.

Answer 1

Ответ:

Площадь боковой поверхности пирамиды равна половине произведения периметра основания и апофемы.

Формула площади боковой поверхности пирамиды:$S_{бок} = \frac{1}{2} P_{осн} l$

Периметр – сумма длин всех сторон. Так как основанием является правильный шестиугольник, у него все стороны равны.

P=6a

P=6×6=36 дм

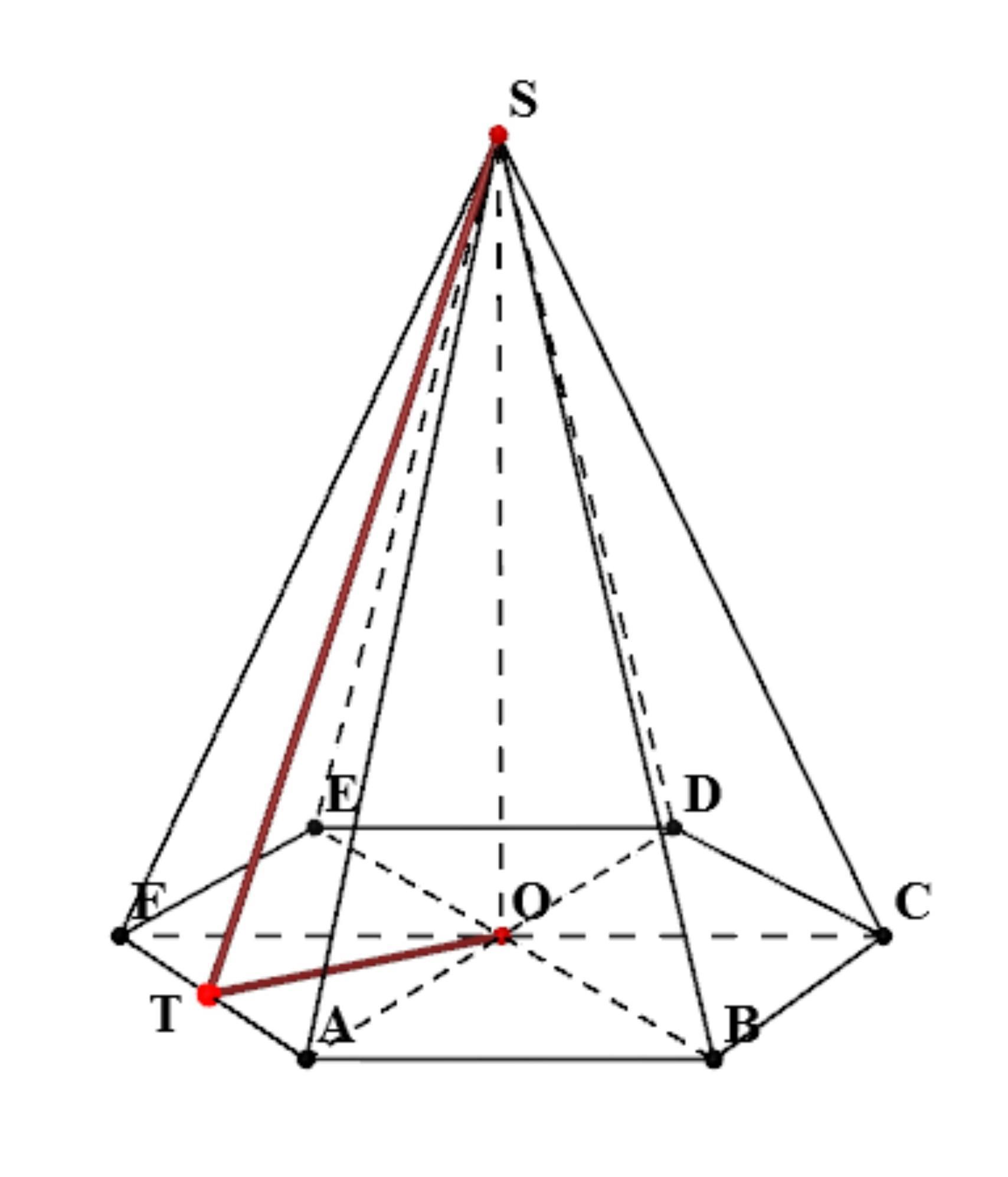
Апофема – это высота боковой грани, опущенная из вершины пирамиды. На чертеже это ST.

Ее найдем по треугольнику SOT. SO – высота пирамиды, а значит SOT – прямоугольный треугольник, где <SOT=90°.

OT – радиус, вписанной окружности в основание.

Формула радиуса вписанной окружности в правильный многоугольник: $r= \frac{a}{2 \tg(\frac{\pi}{n})}$, где a – сторона, n – количество сторон.

$r = \frac{6}{2 \times \tg( \frac{\pi}{6} ) } = \frac{6}{2 \times \frac{1}{ \sqrt{3} } } = \frac{6 \sqrt{3} }{2} = 3 \sqrt{3}$

Радиус вписанной окружности в основание 3√3 дм.

По теореме Пифагора, квадрат гипотенузы равен сумме квадратов катетов, l²=H²+r².

Высота, по условию, 3 дм, а радиус 3√3 дм.

${l}^{2} = {3}^{2} + {(3 \sqrt{3} )}^{2} \\ {l}^{2} = 9 + 27 \\ {l}^{2} = 36 \\ l = \sqrt{36} \\ l = 6$

Апофема равняется 6 дм.

Теперь остается подставить в формулу.

$S_{бок} = \frac{1}{2} \times 36 \times 6 = 108$

Ответ: Площадь боковой поверхности данной пирамиды 108 дм².