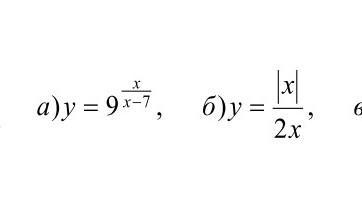Question

Исследовать функцию на непрерывность, классифицировать точки разрыва. ​

Answer 1

Ответ:

а) единственная точка разрыва (разрыва 2-го рода) - это 7.

б) единственная точка разрыва (разрыва 1-го рода) - это 0.

Объяснение:

Как известно, элементарные функции непрерывны на области своего определения (есть точка зрения, что надо говорить про внутренние точки области определения, но  такое уточнение делают только те, кто непрерывность определяет с помощью предела, который должен совпадать со значением функции в точке, но не считает легитимным определение на языке эпсилон-дельта. Впрочем, эти нюансы в наших примерах роли не играют).

a) $y=9^{\frac{x}{x-7}}.$ Область определения: $x\not= 7;$ исследуем только точку 7, поскольку в остальных точках функция непрерывна.

$\lim\limits_{x\to 7-}\dfrac{x}{x-7}=-\infty,$ а поскольку $\lim\limits_{t\to -\infty}9^{t}=0\Rightarrow \lim\limits_{x\to 7-}9^{\frac{x}{x-7}}=0.$

$\lim\limits_{x\to 7+}\dfrac{x}{x-7}=+\infty,$ а поскольку $\lim\limits_{t\to +\infty}9^t=+\infty\Rightarrow \lim\limits_{x\to 7+}9^{\frac{x}{x-7}}=+\infty.$

Предел слева оставлял надежду на разрыв первого рода, но  предел справа заставляет нас признать, что 7 - точка разрыва второго рода.

б) $y=\dfrac{|x|}{2x}.$ Область определения: $x\not=0.$ Достаточно исследовать на непрерывность точку 0.

$\lim\limits_{x\to 0-}\dfrac{|x|}{2x}=\lim\limits_{x\to 0-}\dfrac{-x}{2x}=-\dfrac{1}{2};\ \lim\limits_{x\to 0+}\dfrac{|x|}{2x}=\lim\limits_{x\to 0+}\dfrac{x}{2x}=\dfrac{1}{2}.$

Пределы слева и справа конечные, но не равны друг другу. Поэтому 0 - точка разрыва первого рода (такой разрыв называется еще скачком).