Question

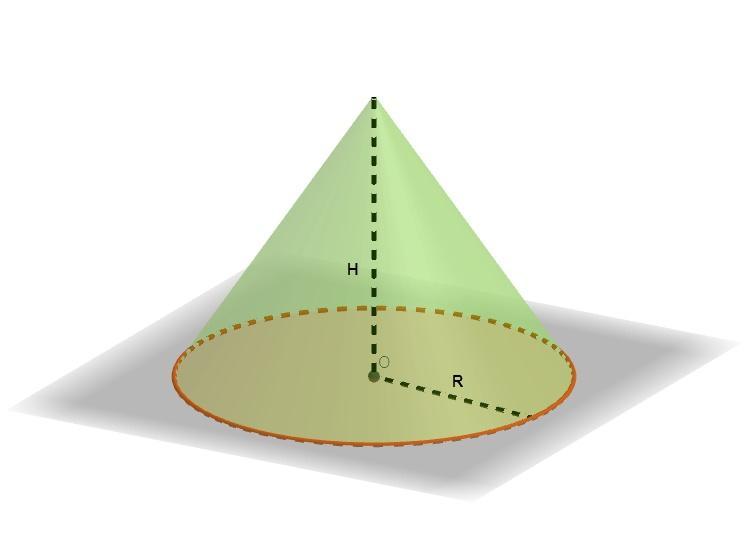
Высоту конуса уменьшили в 9 раз. Во сколько раз надо увеличить радиус основания конуса, чтобы его объем остался прежним?

Answer 1

Ответ:

Чтобы объём конуса остался прежним, нужно увеличить радиус основания в 3 раза.

Объяснение:

Высоту конуса уменьшили в 9 раз. Во сколько раз надо увеличить радиус основания конуса, чтобы его объем остался прежним?

• Объем конуса равен одной трети произведения площади основания на высоту. V=1/3*S*H

Основанием конуса является круг, площадь круга: S=πR².

Поэтому формула для нахождения объёма конуса примет вид:

V=1/3*πR²*H

РЕШЕНИЕ

Пусть первоначальный радиус конуса - R, а первоначальная высота - Н.

Тогда объём первоначального конуса:

V = 1/3*πR²*H

Далее, высоту конуса уменьшили в 9 раз, то есть высота конуса после преобразования: Н/9.

Радиус конуса после преобразования: R₁.

Тогда объём конуса после преобразования:

V₁ = 1/3*πR₁²*H/9

Найдём R₁, если известно, что объём остался прежним:  

V=V₁

$\dfrac{1}{3} \pi R^{2} H=\dfrac{1}{3} \pi R_1^{2} \dfrac{H}{9}$

R²=R₁²/9

R₁²=9R²

$R_1=\sqrt{9R^{2} }$

R₁=3R

Таким образом,  радиус нужно увеличить в 3 раза, чтобы объем остался прежним.

#SPJ1