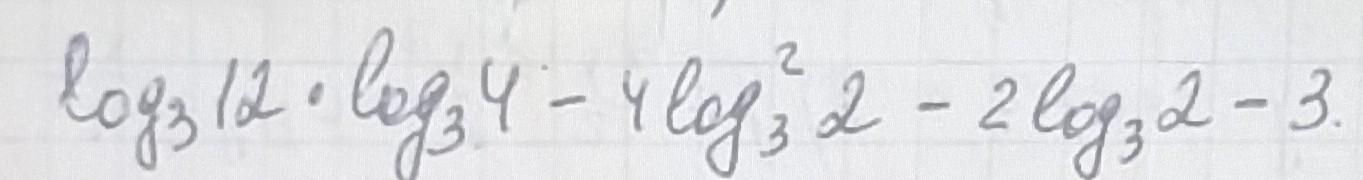Ответы
Ответ дал:
0
Ответ:
Применим свойства логарифма: и
Аноним:
здравствуйте, помогите пожалуйста решить задачу по математике
С помощью двойного интеграла найти объем тела, ограниченного данными поверхностями. Построить данное тело и область интегрирования
Вас заинтересует
2 года назад
2 года назад
7 лет назад
7 лет назад
9 лет назад