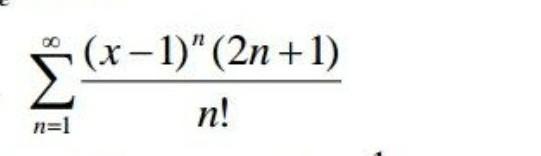Ответы
Ответ дал:
2
Ответ:
Применим признак Даламбера к ряду, составленному из абсолютных величин заданного ряда .
Область сходимости - .
Аноним:
спасибо большое
а дифференциальное уравнение не получается
там начальные условия некорректные
хотя , решу
Вас заинтересует
2 года назад
2 года назад
2 года назад
7 лет назад
9 лет назад