Question

В треугольнике АВС медианы АВ и АС пересекаются в точке D
1) доказать что точка D середина ВС
2) доказать что <А= <В -<С

Answer 1

Ответ:

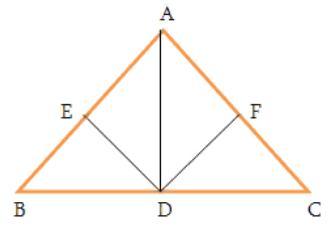
1) В треугольнике ЕВD по теорему Пифагора ВD²=ЕD²+ВЕ²

В треугольнике ЕАD по теорему Пифагора АD²=ЕD²+АЕ²

Поскольку ЕD медиана стороны АВ ⇒ ЕА=ЕВ

так как ЕА=ЕВ ⇒ ВD²=АD²⇒ ВD=АD

В треугольнике FDС по теорему Пифагора

СD²=FD²+FС²

В треугольнике FDА по теорему Пифагора

АD²=DF²+АF²

FD медиана стороны АС ⇒

СD²=АD²⇒

СD=АD

получается что ВD=АD  СD=АD

⇒ ВD=DС

2) Поскольку треугольник DАС равнобедренный ⇔ АD=СD ⇒

∠DАС=∠С

Поскольку треугольник DАВ равнобедренный ⇔ АD=ВD ⇒

∠DАВ=∠В

очевидно что ∠А=∠В+∠С