В треугольнике ABC угол A равен π - arcsin8/17 , сторона BC равна 8. На продолжении CB за точку B взята точка D так, что BD=1 . Найдите радиус окружности, проходящей через вершину A , касающейся прямой BC в точке D и касающейся окружности, описанной около треугольника ABC .
Приложения:
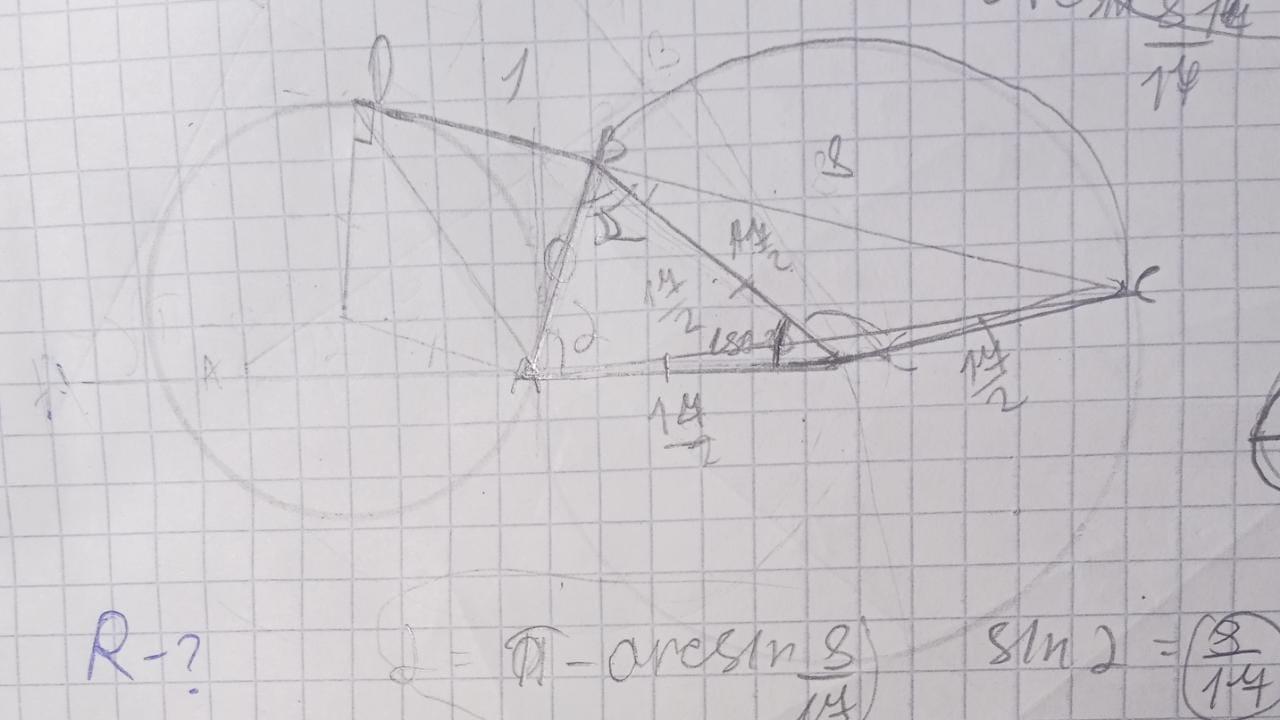
guvanch021272:
условие правильное?
Да
Не уверен. Две окружности касаться могут только в одной точке. Т.е. у них не может быть точек пересечения. По условию каждая из данных окружностей имеют вторую общую точку - А. Значит точка А и есть их точка касания. Точка D лежит извне окружности описанной около треугольника ABC. Тогда получим что эти окружности пересекаются
прикрепил фото
Радиус окружности ABC по т синусов 8,5. Расстояние от центра этой окружности до BC 7,5. Далее т Пифагора: (R+8,5)^2=(R+7,5)^2+5^2 => R=4,5
Ответы
Ответ дал:
0
sinA =sin(π -arcsin(8/17)) =sin(arcsin(8/17)) =8/17
△ABC, т синусов
BC/sinA =2R => 8 :8/17 =2R => R=17/2
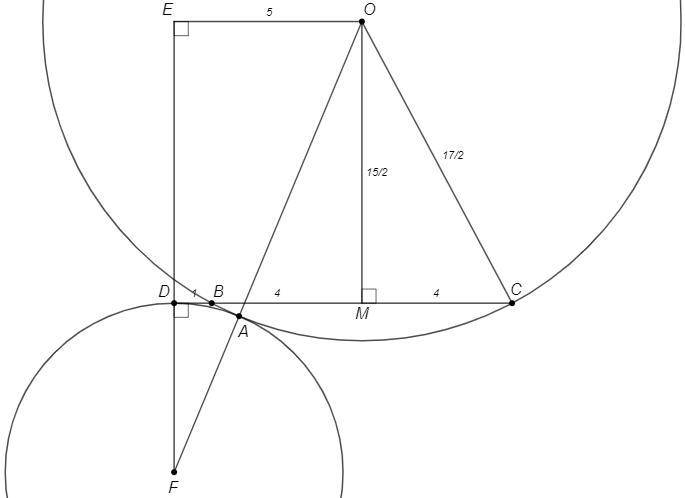
OA=OC =17/2
OM⊥BC, BM=MC=4
△OMC, т Пифагора: OM=15/2
OE=BD+BM=5
FA=FD=x
Точка касания двух окружностей лежит на линии центров.
△OEF, т Пифагора
(FA+OA)^2 =(FD+ED)^2 +OE^2
(x +17/2)^2 =(x +15/2)^2 +25 => 17x +16 =15x +25 => x=9/2
Приложения:
Вас заинтересует
2 года назад
2 года назад
2 года назад
2 года назад
7 лет назад
7 лет назад
9 лет назад