Знайти шлях, що проходить тіло прямолінійно
рухаючись із відомою швидкістю v(t) за час від t1 до t2 . Обчисліть
середню швидкість такого руху.
Приложения:
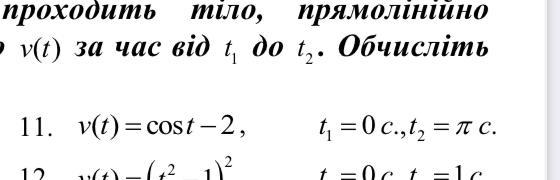
ВикаБач:
Путь это интеграл от скорости, средняя скорость=весь путь/всё время.
Ответы
Ответ дал:
3
Ответ:
За время от 0 с до π с тело прошло путь 2π м.
Средняя скорость движения тела равна 2 м/с.
Объяснение:
Найти путь, который проходит тело прямолинейно, двигаясь со скоростью υ(t) = cost - 2 за время от t₁ = 0 с до t₂ = π с.
Вычислить среднюю скорость этого движения.
- Путь, пройденный телом за промежуток времени от t = a до t = b, равен определенному интегралу от скорости этого тела
- Если график функции находится ниже оси OX, то есть f(x) < 0 на заданном промежутке, то интеграл этой функции берется со знаком минус на этом промежутке:
1) Так как , то
Тогда пройденный телом путь равен значению выражения:
Вычислим путь:
(учитывая, что sinπ = 0; sin0 = 0).
За время от 0 с до π с тело прошло путь 2π м.
2) Средняя скорость движения тела равна отношению всего пройденного пути ко всему затраченному времени:
м/с.
Средняя скорость движения тела равна 2 м/с.
#SPJ1
Вас заинтересует
2 года назад
2 года назад
2 года назад
2 года назад
8 лет назад
8 лет назад
9 лет назад
9 лет назад