Ответы
Ответ дал:
0
Відповідь:
Покрокове пояснення:
фото
Приложения:
Ответ дал:
0
Ответ:
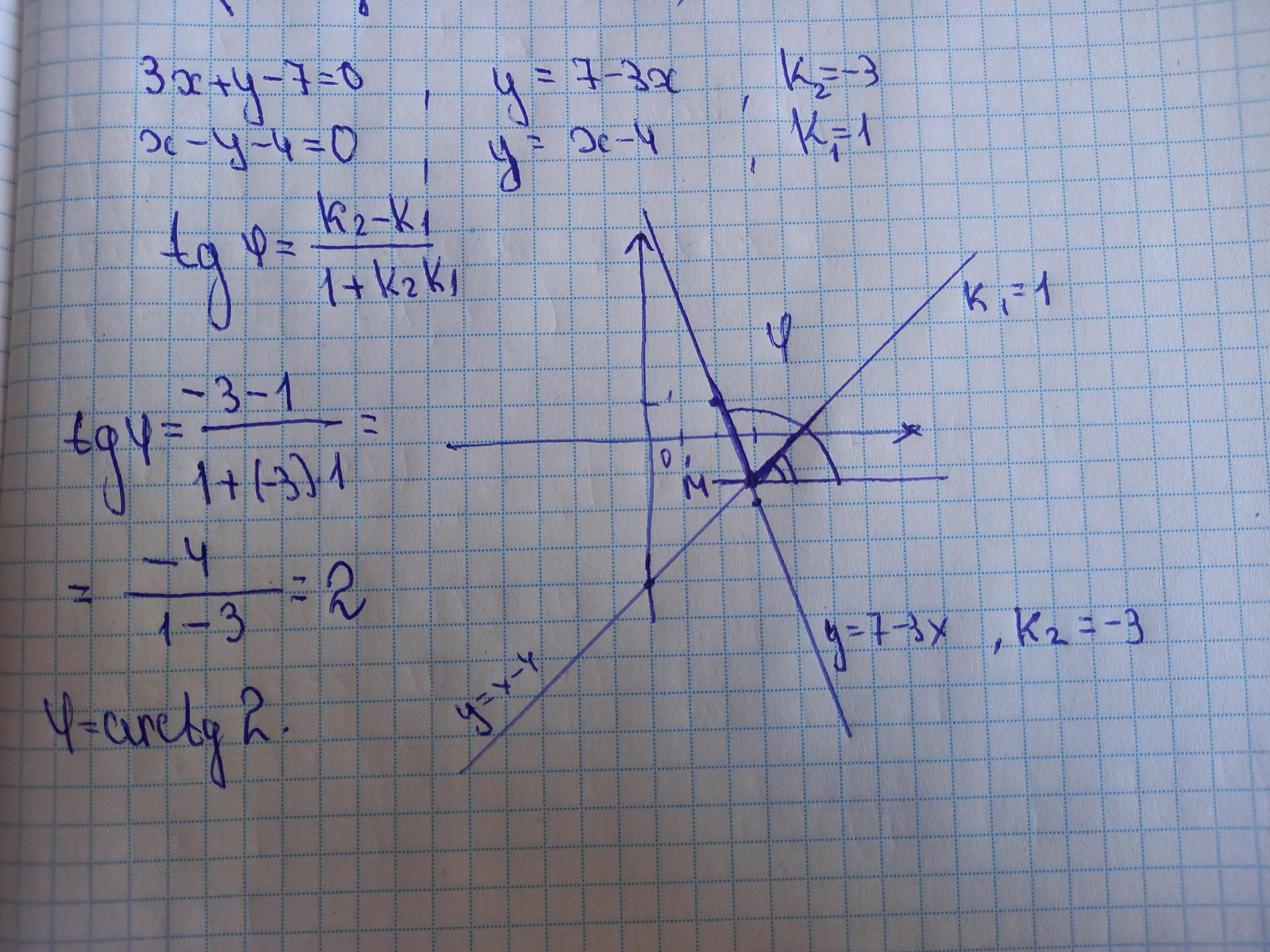
Приведем канонический вид прямой в уравнение с угловым коэффициентом вида y=kx+b.
Получается
Если не знали, то x можно написать, как 1x. Поэтому
Формула тангенса угла между прямыми:
Если , то получается, что в знаменателе будет 0. Тогда угол будет равен 90°, поэтому сначала надо проверить произведение коэффициентов.
Ответ не -1, поэтому находим по формуле.
Вас заинтересует
2 года назад
2 года назад
2 года назад
2 года назад
7 лет назад
9 лет назад