ОЧЕНЬ СРОЧНО! Доказать, что если в треугольнике две медианы взаимно перпендикулярны, то сумма их квадратов равна квадрату третьей медианы. ДАЮ 30 БАЛЛОВ!
Ответы
Ответ дал:
2
Ответ:
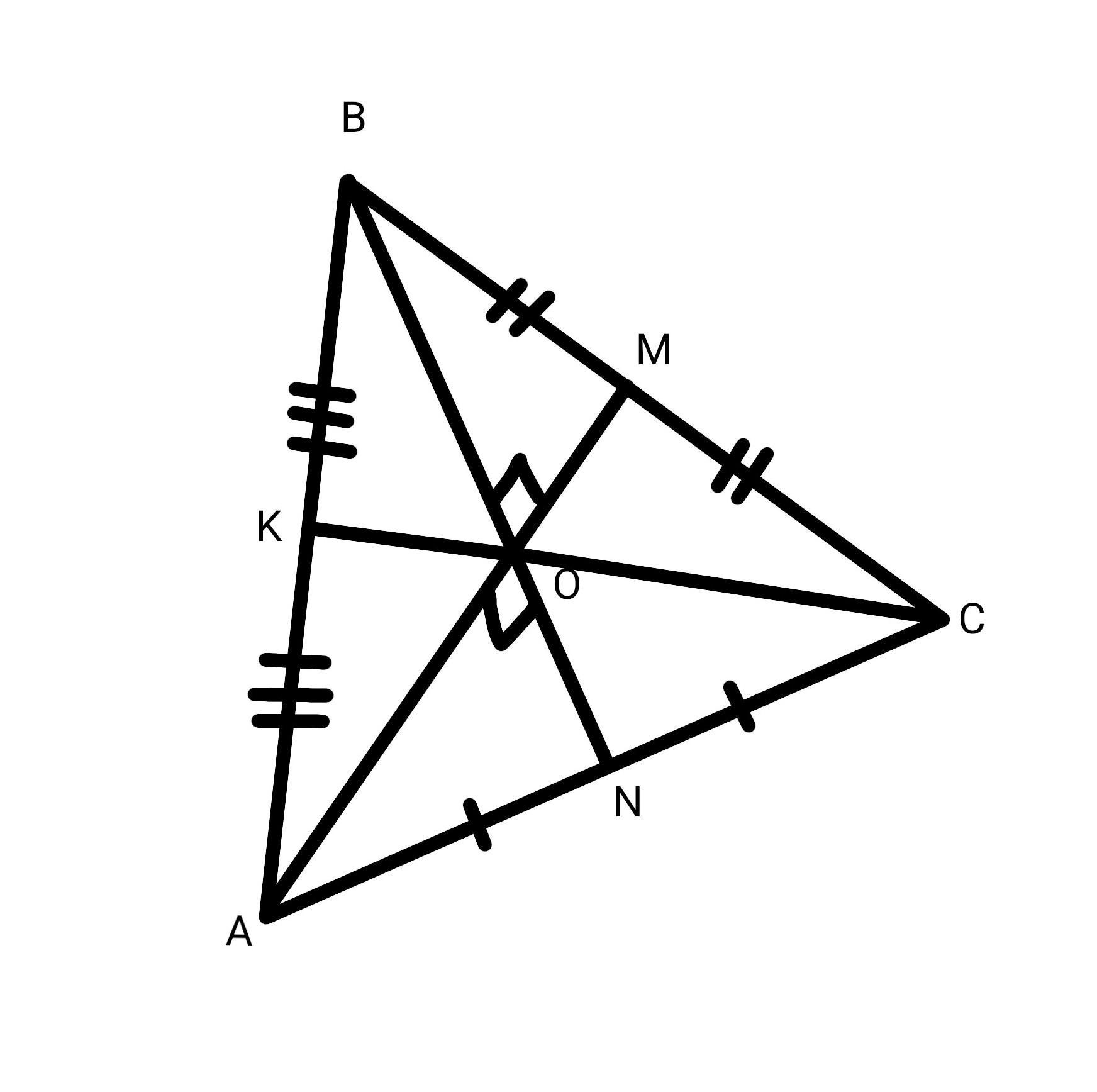
Медианы AM и BN перпендикулярны.
Медиана делится точкой пересечения в отношении 2:1, считая от вершины.
Обозначим AO=2x, OM=x, BO=2y, ON=y.
По теореме Пифагора, квадрат гипотенузы равен сумме квадратов катетов, BM²=BO²+OM².
AN²=AO²+ON²
AB²=AO²+BO²
Формулы длины медианы:
Это длина третьей медианы.
Теперь найдем сумму квадратов двух медиан и приравняем к квадрату третьей.
AM=2x+x=3x
BN=2y+y=3y
Как мы видим
Приложения:
dayanalebedenko8:
Спасибо большое)
Вас заинтересует
2 года назад
2 года назад
2 года назад
7 лет назад
7 лет назад