Question

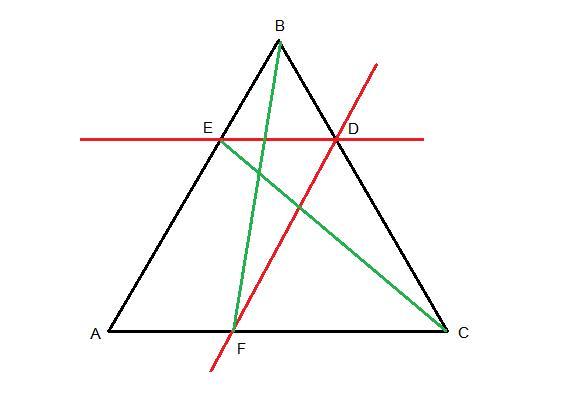
в треугольнике АВC прямые, параллельные другим сторонам, проведены из точки D которая на стороне ВС, эти прямые пересекают стороны АВ и АС в точках Е и F.
Доказать что площадь треугольника СDE равна площади ВDF

Answer 1

По данным

ЕD║АС, DF║АВ

пусть площадь ΔСDЕ = $S$$_{1}$  которая равна $\frac{ED x DCxsin < EDC}{2}$

пусть площадь ΔBDF = $S_{2}$  которая равна $\frac{FDxBDxsin < BDF}{2}$

⇔

$\frac{S_{1} }{S_{2} } = \frac{EDxDCxsin < EDC}{FDxBDxsin < BDF}$

поскольку  накрест лежащие углы при пересечении стороны АВ с сечениями AC и ED равны

⇔

∠BED = ∠BAC, ∠BDE = ∠BCA

⇔

ΔABC = ΔEBD

и поскольку они равны

$\frac{BC}{BD} = \frac{AC}{ED}$ ⇒ $\frac{ED}{BD} = \frac{AC}{BC}$

ΔABC = ΔFDC

⇔

$\frac{AB}{FD} =\frac{BC}{DC}$ ⇒ $\frac{DC}{FD} = \frac{BC}{AB}$

и так как

$\frac{ED}{BD} = \frac{AC}{BC}$, $\frac{DC}{FD} = \frac{BC}{AB}$

⇒

$\frac{S_{1} }{S_{2} } = \frac{EDxDCxsin < EDC}{FDxBDxsin < BDF} = \frac{ACxBCxsin < EDC}{ABxBCxsin < BDF} = \frac{ACxsin < EDC}{ABxsinBDF}$

замечаем что четырехугольники AEDC, ABDF трапеции ⇒

∠EDC + ∠ACD = 180°

∠BDF + ∠ABD = 180°

⇔

∠EDC = 180° - ∠ACD = 180° - ∠ACB

∠BDF = 180° - ∠ABD = 180° - ∠ABC

⇔

sin∠EDC = sin ( 180° - ∠ACB ) = sin∠ACB

sin∠BDF = (180° - ∠ABC ) = sin∠ABC

$\frac{S_{1} }{S_{2} } = \frac{ACx sin < EDC}{ABxsin < BDF} = \frac{ACxsin < ACB}{ABx sin < ABC}$

В треугольнике  АВС по теорему синусов

$\frac{AC}{AB} = \frac{sin < ABC}{sin < ACB}$

⇔

$\frac{S_{1} }{S_{2} } = \frac{ACxsin < ACB}{ABxsin < ABC} = \frac{sin < ABC}{sin < ACB} x \frac{sin,ACB}{sin < ABC} = 1$

⇔

$S_{1} = S_{2}$

Answer 2

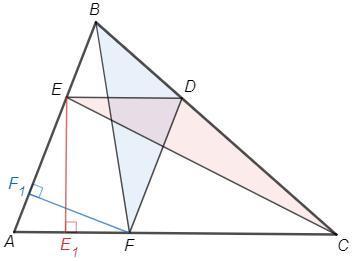
AEDF - параллелограмм, EE1 и FF1 - высоты

S(AEDF) =ED*EE1 =DF*FF1

S(CDE) =1/2 ED*EE1

S(BDF) =1/2 DF*FF1

=> S(CDE) =S(BDF)