Выберете правильное решение уравнения:\( 2tg³x - 2tg²x + 3tgx - 3 = 0 Выберите один ответ: \( x = 4 + "n, neZ - \(x= \frac{ \pi}{4}+ \pi n, n \epsilon Z \(x= \frac{ \pi}{4}+2 \pi n, n \epsilon Z \( x = 4 +n, neZ
Ответы
Ответ дал:
1
Ответ:
решение смотри на фотографии
Приложения:
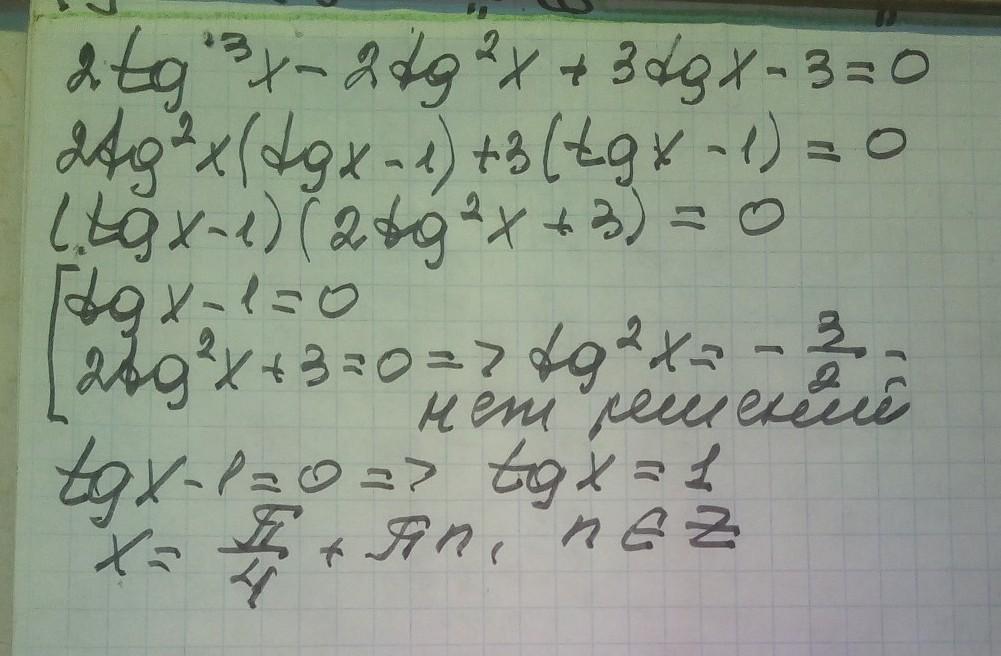
tamilaamangeldina87:
спасибо большое
Ответ дал:
1
Ответ:
Разложим левую часть равенства на множители .
Квадрат любого выражения не может быть отрицательным, поэтому уравнение не имеет решений .
Ответ:
спасибо большое
Вас заинтересует
2 года назад
2 года назад
2 года назад
7 лет назад
7 лет назад
9 лет назад
9 лет назад