Question

найти площадь трапеции с основаниями АВ и СД
если
1) АВ = 10sm
BC = AD = 13sm
CD = 20sm

2) AB = 6sm
BC = 9√2

Answer 1

Ответ:

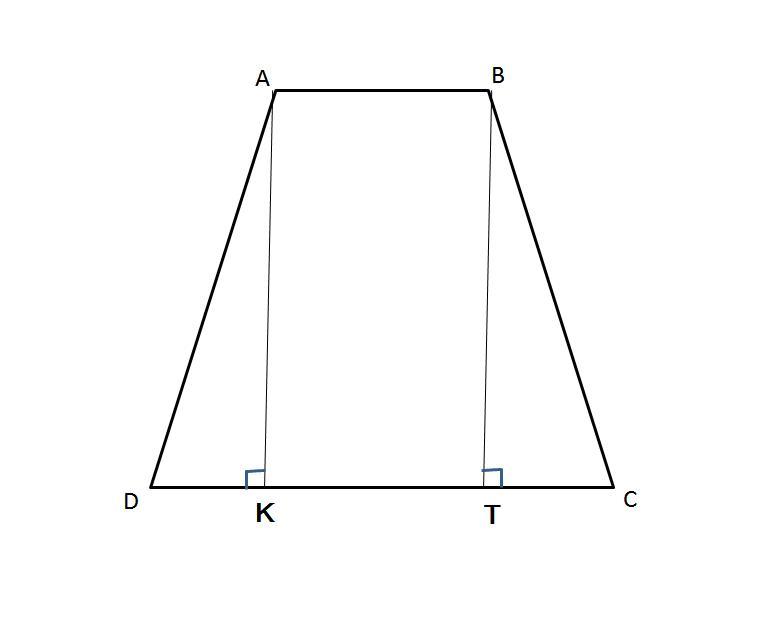
AK, BT ║CD

1) поскольку трапеция равнобедренный то есть ВС = АD

=> DK = TC

AB = KT = CD - ( DK + TC )

DK + TC = CD - AB

DK + TC = 20 - 10 = 10см

=>

DK = TC = 1/2 · 10 = 5см

Из прям треугольника АDК

по теорему Пифагора

AD² = AK² + DK²

AK² = AD² - DK²

AK = √AD² - DK² = √169 - 25 = √144

AK = 12

S = a + b/ 2 ·h

S = 10 + 20 /2 ·12 = 180см²

2) ∠C = ∠D = 45° => трапеция равнобедренная

=> AD = BC = 9√2

из прям. треугольника ADK

AK = AD · sin∠D

DK = AD · cos∠D

AK = 9√2 · sin45° = 9√2 · √2/2 = 9см

DK = 9√2 · cos45° =  9√2 · √2/2  = 9см

AD = BC =>

TC = DK = 9см

CD = AB + ( DK + TC ) = 24

S = AB + CD /2 · AK = 6 + 34 /2 · 9 = 135см²