Ответы
Ответ дал:
4
Ответ:
2√3 ед²
Пошаговое объяснение:
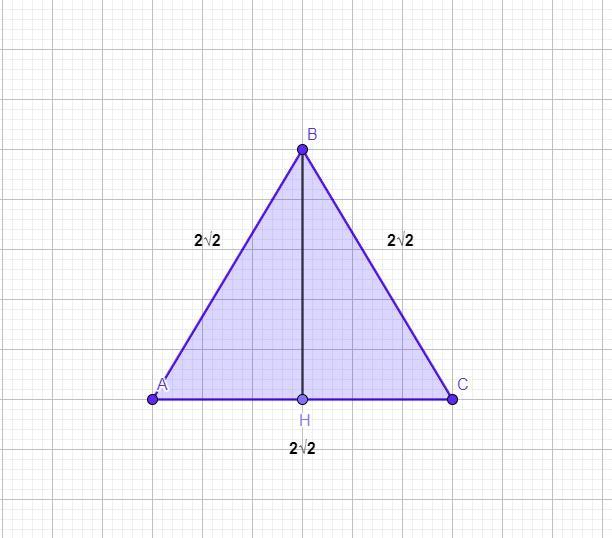
Проведём высоту ВН⊥АС в равностороннем ΔАВС.
Так как равносторонний треугольник является частным случаем равнобедренного, то высота ВН является также медианой. АН=НС=2√2:2=√2
ΔВСН(∠Н=90°)
По теореме Пифагора: ВН²=ВС²-НС²=(2√2)²-(√2)²=8-2=6
ВН=√6=2
Тогда:
Или есть готовая формула для нахождения площади равностороннего треугольника:
Приложения:
Вас заинтересует
2 года назад
2 года назад
2 года назад
8 лет назад
8 лет назад
9 лет назад
9 лет назад