Question

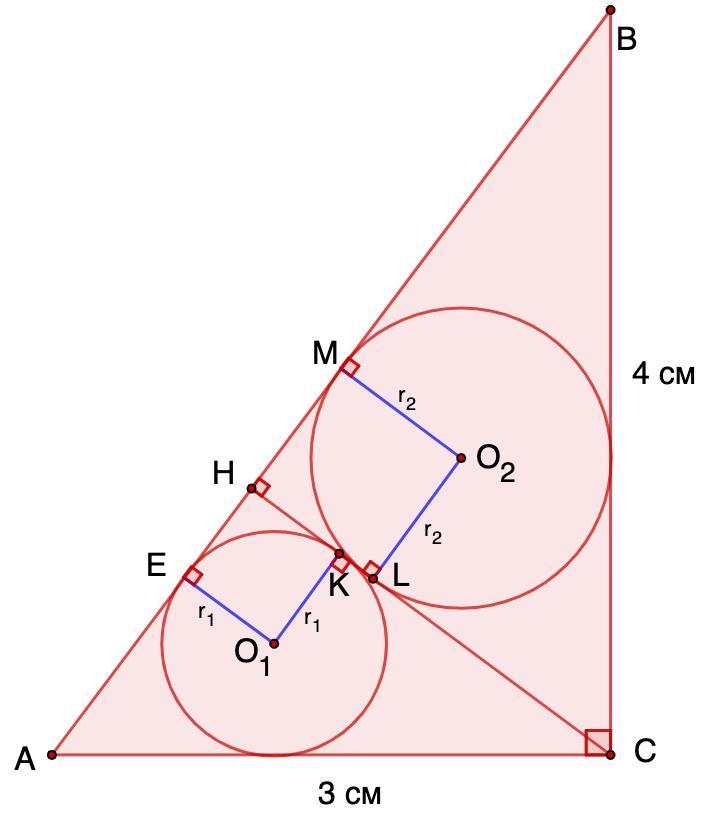
В прямокутному трикутнику АВС (С=90°) з катетами 3 і 4 см провели висоту СН. У отримані трикутники АСН і ВСН вписали дві окружності, які дотикаються СН в точках К і L. Знайти довжину відрізка KL. Срочно!!!!!!!

Answer 1

Ответ:

Длина отрезка KL равна 0,2 см.

Объяснение:

В прямоугольном треугольнике АВС (∠С = 90°) с катетами 3 и 4 см провели высоту СН. В полученные треугольники АСН и ВСН вписали две окружности, которые соприкасаются СН в точках К и L. Найти длину отрезка KL.

Дано: ΔАВС - прямоугольный;

∠С = 90°;

СН - высота;

АС = 3 см; ВС = 4 см.

Окр.О₁, r₁ - вписана в ΔАНС;

Окр.О₂, r₂ - вписана в ΔСНВ.

К - точка касания Окр.О₁, r₁  и СН;

L - точка касания Окр.О₂, r₂  и СН.

Найти: KL.

Решение:

1. Рассмотрим ЕНКО₁.

СН ⊥ АВ (высота);

• Радиус, проведенный в точку касания, перпендикулярен касательной.

⇒ О₁Е ⊥ АН; О₁К ⊥ СН.

⇒ ЕНКО₁ - прямоугольник.

• Противоположные стороны прямоугольника равны.

⇒ О₁Е = НК = r₁.

2. Рассмотрим LHMO₂.

СН ⊥ АВ (высота);

⇒ O₂M ⊥ НB; О₂L ⊥ СН (радиусы, проведенные в точку касания).

⇒ LHMO₂ - прямоугольник.

О₂М = LH = r₂.

Искомый отрезок KL = HL - HK = r₂ - r₁

Радиус окружности, вписанной в прямоугольный треугольник, равен:

         $\displaystyle\bf \boxed {r=\frac{a+b-c}{2} }$ ,

где a и b - катеты, с - гипотенуза.

3. Рассмотрим ΔАВС - прямоугольный.

По теореме Пифагора найдем АВ:

АВ² = АС² + СВ² = 9 + 16 = 25

АВ = √25 = 5 (см)

Теперь используем метрические соотношения в прямоугольном треугольнике:

• Квадрат высоты прямоугольного треугольника, проведенной к гипотенузе, равен произведению проекций катетов на гипотенузу, а квадрат катета равен произведению гипотенузы и проекции этого катета на гипотенузу.

⇒

АС² = АН · АВ

9 = АН · 5

$\displaystyle\bf AH=\frac{9}{5}\;_{(CM)} \\\\HB=AB - AH=5-\frac{9}{5}=\frac{16}{5}\;_{(CM)}$

$\displaystyle\bf CH^2=AH\cdot{HB}=\frac{9}{5}\cdot\frac{16}{5} \\ \\CH=\sqrt{\frac{9\cdot16}{25} } =\frac{12}{5}\;_{(CM)}$

4. Рассмотрим ΔАНС - прямоугольный.

$\displaystyle\bf r_1=\frac{AH+HC-AC}{2} =\frac{\frac{9}{5}+\frac{12}{5}-3 }{2}=\\ \\=\frac{6}{10}=0,6\;_{(CM)}$

5. Рассмотрим ΔCHB - прямоугольный.

$\displaystyle\bf r_2=\frac{BH+HC-BC}{2} =\frac{\frac{16}{5}+\frac{12}{5}-4 }{2}=\\ \\=\frac{8}{10}=0,8\;_{(CM)}$

⇒ KL = r₂ - r₁ = 0,8 - 0,6 = 0,2 (см)

Длина отрезка KL равна 0,2 см.

#SPJ1