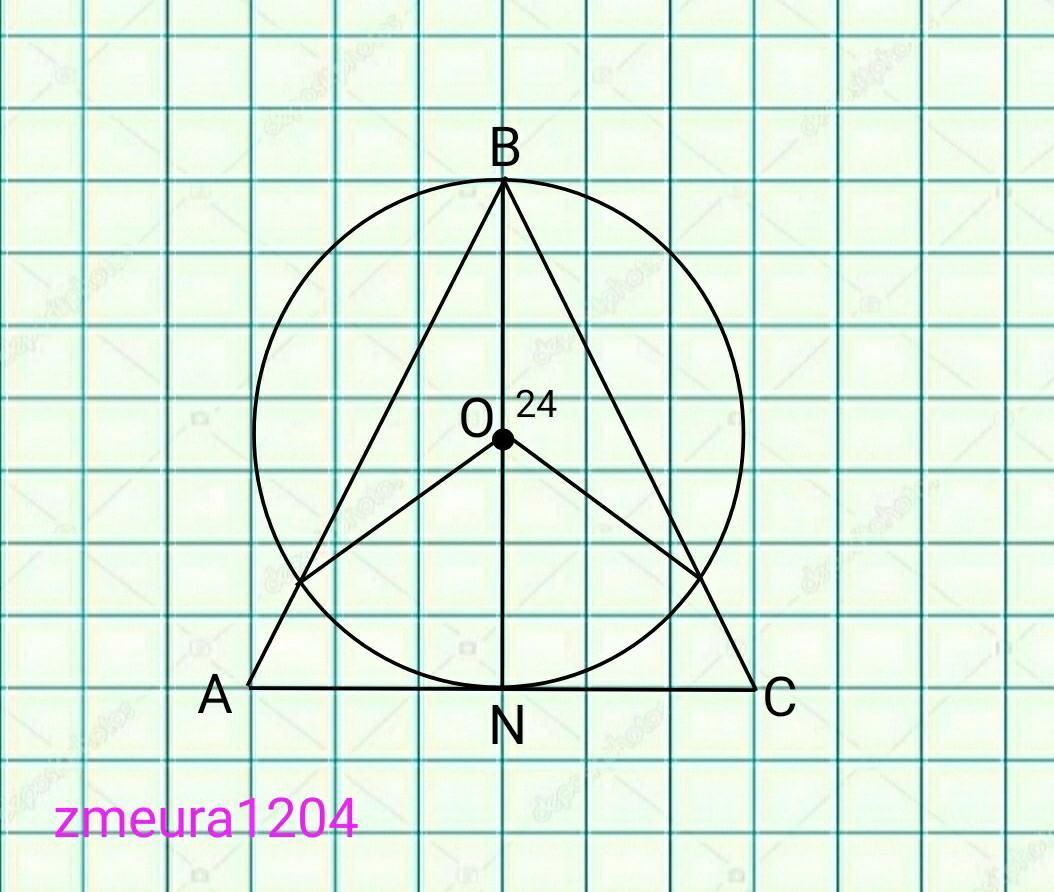
Задан равнобедренный треугольник ABC с углом A = 80° при основании AC. Из вершины B проведена высота BN, равная 24 см. На данной высоте BN, как на диаметре, проведена окружность. Найдите длину дуги окружности, которая принадлежит треугольнику.
Ответы
Ответ дал:
1
Ответ:
8π/3 см
Объяснение:
R=BN/2=24/2=12см.
Сумма углов в треугольнике равна 180°;
В равнобедренном треугольнике углы при основании равны.
∠А=∠С=80°
∠В=180°-2*∠А=180°-2*80°=
=180°-160°=20°
∠В- вписанный угол, тогда центральный угол будет 20°*2=40° угол дуги.
Сдуги=2πR*a°/360°, где а°- центральный угол.
Сдуги=2π*12*40°/360°=24π*1/9=8π/3см
Приложения:
zmeura1204:
Извините не дописала решение, подождите я исправлю.
Вас заинтересует
2 года назад
2 года назад
2 года назад
2 года назад
8 лет назад
8 лет назад