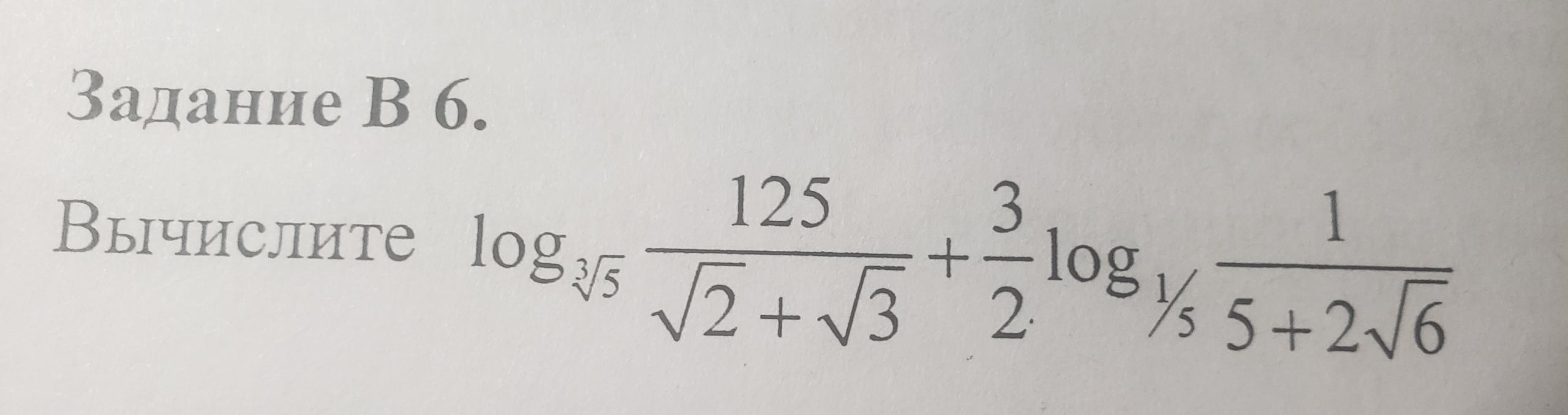Ответы
Ответ дал:
1
Відповідь:
Пояснення:
Приложения:

Ответ дал:
1
Ответ: 9 .
Вычислим каждое слагаемое по отдельности , применяя свойства логарифмов .
Теперь вычислим заданное выражение .
Вас заинтересует
2 года назад
2 года назад
2 года назад
2 года назад
7 лет назад
9 лет назад