Question

12.З деякої точки простору проведено до площини дві похилі. Одна із них дорівнює 16 см і утворює з площиною кут 30°. Знайдіть довжину іншої похилої, якщо її проекція на площину дорівнює 6 см.
а)10√3 см
б)12√3 см
в)12 см
г)10 см

Answer 1

Ответ:

10 см.

Объяснение:

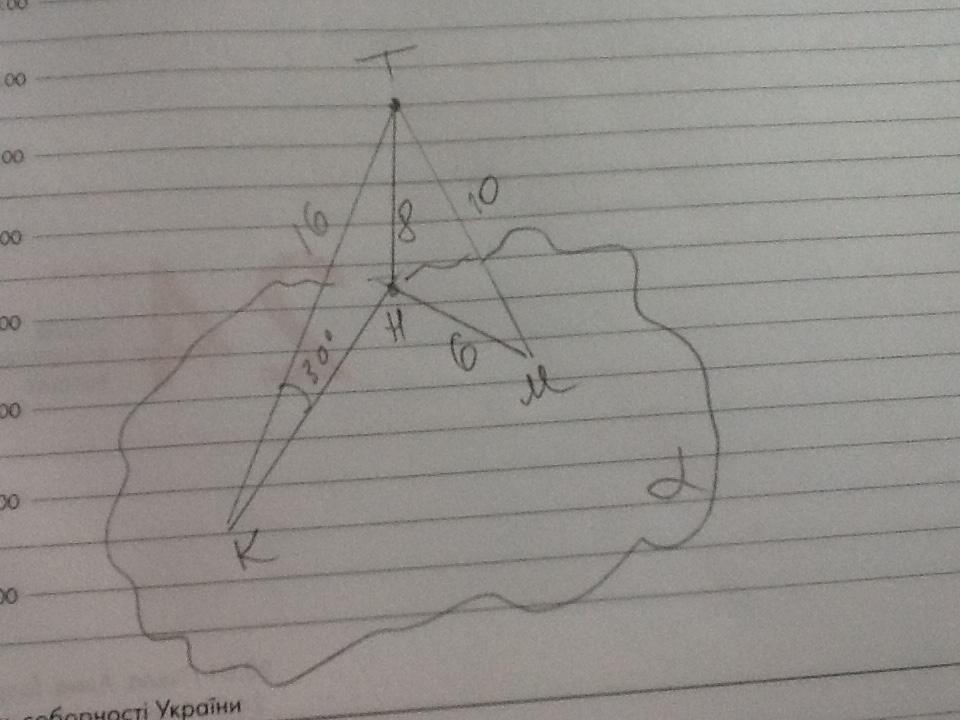
Дано: площина α; точка Т;  ТК=16 см,  ∠НКТ=30°,  МН=6 см.  ТМ - ?

ТН лежить проти кута 30°, отже ТН=1/2 ТК=16:2=8 см.

ΔТМН - прямокутний, ТН=8 см, МН=6 см, отже ТМ=10 см (єгипетський трикутник)

Answer 2

Ответ:

10 см

---------------

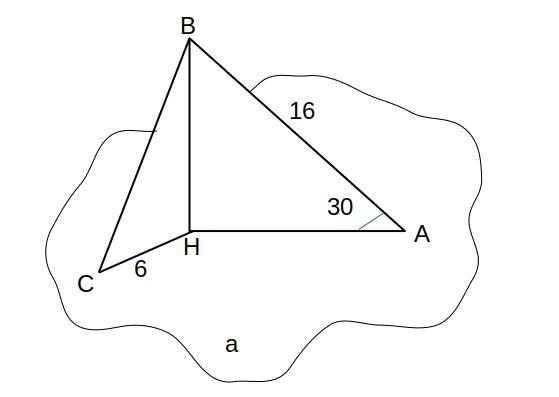
BН⊥ (пл.)α  

=>

BН ⊥ каждой прямой из этой плоскости

НА - проекция наклонной ВА на (пл.) α

ВН⊥НА

из  ΔBАН

∠ВАН=30°  

∠ВНА=90°

ВА = 16 см

поскольку катет, лежащий против угла в 30° равен половине гипотенузы ⇒

ВН=16:2= 8 см

СВ - наклонная

СН - проекция СВ на (пл.) α

СН=5 см ,

из ΔВМН

по теореме Пифагора:

c² = a² + b²

СВ²=СН²+ВН²

СВ=√(СН²+ВН²)=√(6²+8²)=√(36 + 64) = √100=10 см