Ответы
Ответ дал:
1
Ответ:
решение смотри на фотографии
Приложения:

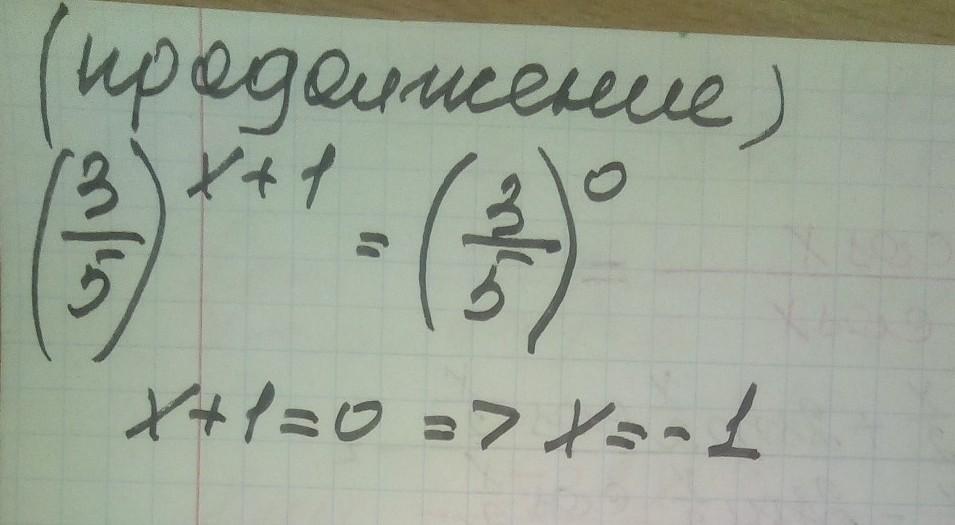
Ответ дал:
1
Ответ:
Воспользуемся свойством .
Делим на .
Основания показательных функций равны, значит равны и показатели.
Вас заинтересует
2 года назад
2 года назад
2 года назад
2 года назад
7 лет назад
9 лет назад
9 лет назад
