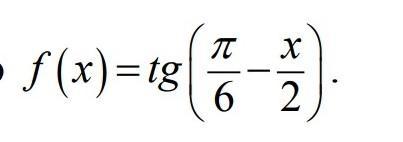Question

Знайдіть похідну функції f , якщо​

Answer 1

Ответ:

f(x) = tg(π/6 - x/2)

f ` (x) = (tg(π/6 - x/2)) ` = 1/(cos^2(π/6 - x/2)) × (π/6 - 1/2x) ` = 1/(cos^2(π/6-x/2)) × (-1/2) = - 1/2/(cos^2(π/6-x/2))

Answer 2

Ответ:

Производная сложной функции тангенс:  $\boldsymbol{(tg\, u)'=\dfrac{1}{cos^2\, u}\cdot u'}$   .

$\displaystyle f(x)=tg\Big(\frac{\pi}{6}-\frac{x}{2}\Big)\ \ ,\ \ \ \ \ \ u=\frac{\pi}{6}-\frac{x}{2}\\\\\\f'(x)=\frac{1}{cos^2\Big(\dfrac{\pi}{6}-\dfrac{x}{2}\Big)}\cdot \Big(-\frac{1}{2}\Big)=\bf -\frac{1}{2\, cos^2\Big(\dfrac{\pi}{6}-\dfrac{x}{2}\Big)}$